![\includegraphics[width=0.45\linewidth]{cpgap}](img2501.png)
|
According to W.J.Getsinger [56] a coplanar series gap (see fig. 12.5) is supposed to be the dual problem of the inductance of a connecting strip between twin strip lines.
The inductance of such a thin strip with a width ![]() and the length
and the length
![]() is given to a good approximation by
is given to a good approximation by
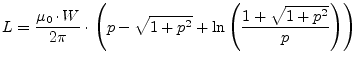 |
(12.32) |
where ![]() and
and
![]() . Substituting this inductance
by its equivalent capacitance of the gap in CPW yields
. Substituting this inductance
by its equivalent capacitance of the gap in CPW yields
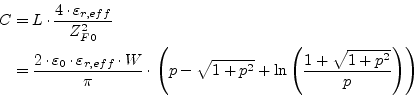 |
(12.33) |