![\includegraphics[width=0.6\linewidth]{cpshort}](img2495.png)
|
There is a similar simple approximation for a coplanar waveguide short-circuit, also given in [54]. The short circuit is inductive in nature.
The equivalent length extension ![]() associated with the
fringing fields is
associated with the
fringing fields is
Equation (12.29) is valid when the metalization thickness
![]() does not become too large (
does not become too large (![]() ).
).
The short end inductance ![]() can be written in terms of the
inductance per unit length and the wave resistance.
can be written in terms of the
inductance per unit length and the wave resistance.
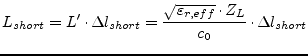 |
(12.30) |
According to W.J.Getsinger [55] the CPW short-circuit inductance per unit length can also be modeled by
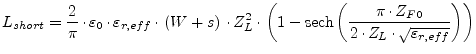 |
(12.31) |
based on his duality [56] theory.