A microstrip open end can be modeled by a longer effective microstrip
line length ![]() as described by M. Kirschning, R.H. Jansen and
N.H.L. Koster [35].
as described by M. Kirschning, R.H. Jansen and
N.H.L. Koster [35].
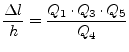 |
(11.185) |
with
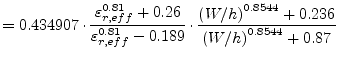 |
(11.186) | |
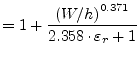 |
(11.187) | |
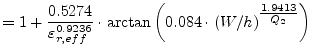 |
(11.188) | |
| (11.189) | ||
| (11.190) |
The numerical error is less than ![]() % for
% for
![]() and
and
![]() .
.
Another microstrip open end model was published by E. Hammerstad [36]:
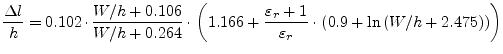 |
(11.191) |
Here the numerical error is less than ![]() % for
% for ![]() .
.
In order to simplify calculations, the equivalent additional line
length ![]() can be transformed into an equivalent open end
capacitance
can be transformed into an equivalent open end
capacitance ![]() :
:
With ![]() being the capacitance per length and
being the capacitance per length and ![]() = 299 792 458 m/s
being the vacuum light velocity.
= 299 792 458 m/s
being the vacuum light velocity.