|
Qucs-core
0.0.18
|
|
Qucs-core
0.0.18
|
Namespaces | |
| device | |
| emi | |
| eqn | |
| fourier | |
| transient | |
Data Structures | |
| class | acsolver |
| class | ptrlist |
| class | analysis |
| class for performing circuit analyses. More... | |
Functions | |
| static void | euclidian_update (nr_double_t a, nr_double_t &n, nr_double_t &scale) |
| template<typename nr_type_t > | |
| nr_type_t | cond_conj (nr_type_t t) |
| template<> | |
| double | cond_conj (double t) |
| static nr_double_t | givens (nr_double_t a, nr_double_t b, nr_double_t &c, nr_double_t &s) |
| Helper function computes Givens rotation. More... | |
| static char * | Cplx2String (nr_complex_t c) |
| nr_complex_t | cos (const nr_complex_t z) |
| Compute complex cosine. More... | |
| nr_complex_t | sin (const nr_complex_t z) |
| Compute complex sine. More... | |
| nr_complex_t | tan (const nr_complex_t z) |
| Compute complex tangent. More... | |
| nr_complex_t | acos (const nr_complex_t z) |
| Compute complex arc cosine. More... | |
| nr_complex_t | asin (const nr_complex_t z) |
| Compute complex arc sine. More... | |
| nr_complex_t | atan (const nr_complex_t z) |
| Compute complex arc tangent. More... | |
| nr_complex_t | cosh (const nr_complex_t z) |
| Compute complex hyperbolic cosine. More... | |
| nr_complex_t | sinh (const nr_complex_t z) |
| Compute complex hyperbolic sine. More... | |
| nr_complex_t | tanh (const nr_complex_t z) |
| Compute complex hyperbolic tangent. More... | |
| nr_complex_t | acosh (const nr_complex_t z) |
| Compute complex arc hyperbolic cosine. More... | |
| nr_complex_t | asinh (const nr_complex_t z) |
| Compute complex arc hyperbolic sine. More... | |
| nr_complex_t | atanh (const nr_complex_t z) |
| Compute complex arc hyperbolic tangent. More... | |
| nr_complex_t | exp (const nr_complex_t z) |
| Compute complex exponential. More... | |
| nr_complex_t | log (const nr_complex_t z) |
| Compute principal value of natural logarithm of z. More... | |
| nr_complex_t | log10 (const nr_complex_t z) |
| Compute principal value of decimal logarithm of z. More... | |
| nr_complex_t | pow (const nr_complex_t z, const nr_double_t d) |
| Compute power function with real exponent. More... | |
| nr_complex_t | pow (const nr_double_t d, const nr_complex_t z) |
| Compute power function with complex exponent but real mantisse. More... | |
| nr_complex_t | pow (const nr_complex_t z1, const nr_complex_t z2) |
| Compute complex power function. More... | |
| nr_complex_t | sqrt (const nr_complex_t z) |
| Compute principal value of square root. More... | |
| nr_double_t | norm (const nr_complex_t z) |
| Compute euclidian norm of complex number. More... | |
| nr_complex_t | cot (const nr_complex_t z) |
| Compute complex cotangent. More... | |
| nr_complex_t | acot (const nr_complex_t z) |
| Compute complex arc cotangent. More... | |
| nr_complex_t | coth (const nr_complex_t z) |
| Compute complex hyperbolic cotangent. More... | |
| nr_complex_t | acoth (const nr_complex_t z) |
| Compute complex argument hyperbolic cotangent. More... | |
| nr_complex_t | sech (const nr_complex_t z) |
| Compute complex hyperbolic secant. More... | |
| nr_complex_t | asech (const nr_complex_t z) |
| Compute complex argument hyperbolic secant. More... | |
| nr_complex_t | cosech (const nr_complex_t z) |
| Compute complex argument hyperbolic cosec. More... | |
| nr_complex_t | atan2 (const nr_complex_t y, const nr_complex_t x) |
| Compute complex arc tangent fortran like function. More... | |
| nr_complex_t | log2 (const nr_complex_t z) |
| Compute principal value of binary logarithm of z. More... | |
| nr_complex_t | signum (const nr_complex_t z) |
| complex signum function More... | |
| nr_complex_t | sign (const nr_complex_t z) |
| complex sign function More... | |
| nr_complex_t | sinc (const nr_complex_t z) |
| Cardinal sine. More... | |
| nr_double_t | xhypot (const nr_complex_t a, const nr_complex_t b) |
| Euclidean distance function for complex argument. More... | |
| nr_double_t | xhypot (nr_double_t a, nr_complex_t b) |
| Euclidean distance function for a double b complex. More... | |
| nr_double_t | xhypot (nr_complex_t a, nr_double_t b) |
| Euclidean distance function for b double a complex. More... | |
| nr_complex_t | round (const nr_complex_t z) |
| Complex round Round is the nearest integral value Apply round to real and imaginary part. More... | |
| nr_complex_t | trunc (const nr_complex_t z) |
| Complex trunc Apply round to integer, towards zero to real and imaginary part. More... | |
| nr_double_t | dB (const nr_complex_t z) |
Magnitude in dB Compute 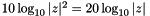 . More... . More... | |
| nr_complex_t | limexp (const nr_complex_t z) |
| Compute limited complex exponential. More... | |
| nr_complex_t | polar (const nr_double_t mag, const nr_double_t ang) |
| Construct a complex number using polar notation. More... | |
| nr_complex_t | polar (const nr_complex_t a, const nr_complex_t p) |
| Extension of polar construction to complex. More... | |
| nr_complex_t | ztor (const nr_complex_t z, nr_complex_t zref) |
| Converts impedance to reflexion coefficient. More... | |
| nr_complex_t | rtoz (const nr_complex_t r, nr_complex_t zref) |
| Converts reflexion coefficient to impedance. More... | |
| nr_complex_t | ytor (const nr_complex_t y, nr_complex_t zref) |
| Converts admittance to reflexion coefficient. More... | |
| nr_complex_t | rtoy (const nr_complex_t r, nr_complex_t zref) |
| Converts reflexion coefficient to admittance. More... | |
| nr_complex_t | floor (const nr_complex_t z) |
| Complex floor. More... | |
| nr_complex_t | ceil (const nr_complex_t z) |
| Complex ceil Ceil is the smallest integral value not less than argument Apply ceil to real and imaginary part. More... | |
| nr_complex_t | fix (const nr_complex_t z) |
| Complex fix. More... | |
| nr_complex_t | fmod (const nr_complex_t x, const nr_complex_t y) |
| Complex fmod Apply fmod to the complex z. More... | |
| nr_complex_t | sqr (const nr_complex_t z) |
| Square of complex number. More... | |
| nr_complex_t | step (const nr_complex_t z) |
| Heaviside step function for complex number. More... | |
| nr_complex_t | cbesselj (unsigned int n, nr_complex_t z) |
| Main entry point for besselj function. More... | |
| static nr_complex_t | cbesselj_smallarg (unsigned int n, nr_complex_t z) |
| static nr_complex_t | cbesselj_mediumarg_odd (unsigned int n, nr_complex_t z) |
| static nr_complex_t | cbesselj_mediumarg_even (unsigned int n, nr_complex_t z) |
| static nr_complex_t | cbesselj_mediumarg (unsigned int n, nr_complex_t z) |
| static nr_complex_t | cbesselj_largearg (unsigned int n, nr_complex_t z) |
| besselj for large argument More... | |
| nr_complex_t | jn (const int n, const nr_complex_t z) |
| Bessel function of first kind. More... | |
| nr_complex_t | yn (const int n, const nr_complex_t z) |
| Bessel function of second kind. More... | |
| nr_complex_t | i0 (const nr_complex_t z) |
| Modified Bessel function of first kind. More... | |
| nr_complex_t | erf (const nr_complex_t z) |
| Error function. More... | |
| nr_complex_t | erfc (const nr_complex_t z) |
| Complementart error function. More... | |
| nr_complex_t | erfinv (const nr_complex_t z) |
| Inverse of error function. More... | |
| nr_complex_t | erfcinv (const nr_complex_t z) |
| Inverse of complementart error function. More... | |
| nr_complex_t | operator% (const nr_complex_t z1, const nr_complex_t z2) |
| Modulo. More... | |
| nr_complex_t | operator% (const nr_complex_t z1, const nr_double_t r2) |
| Modulo. More... | |
| nr_complex_t | operator% (const nr_double_t r1, const nr_complex_t z2) |
| Modulo. More... | |
| bool | operator== (const nr_complex_t z1, const nr_complex_t z2) |
| Equality of two complex. More... | |
| bool | operator!= (const nr_complex_t z1, const nr_complex_t z2) |
| Inequality of two complex. More... | |
| bool | operator>= (const nr_complex_t z1, const nr_complex_t z2) |
| Superior of equal. More... | |
| bool | operator<= (const nr_complex_t z1, const nr_complex_t z2) |
| Inferior of equal. More... | |
| bool | operator> (const nr_complex_t z1, const nr_complex_t z2) |
| Superior. More... | |
| bool | operator< (const nr_complex_t z1, const nr_complex_t z2) |
| Inferior. More... | |
| matrix | operator+ (matrix a, matrix b) |
| Matrix addition. More... | |
| matrix | operator- (matrix a, matrix b) |
| Matrix subtraction. More... | |
| matrix | operator* (matrix a, nr_complex_t z) |
| Matrix scaling complex version. More... | |
| matrix | operator* (nr_complex_t z, matrix a) |
| Matrix scaling complex version (different order) More... | |
| matrix | operator* (matrix a, nr_double_t d) |
| Matrix scaling complex version. More... | |
| matrix | operator* (nr_double_t d, matrix a) |
| Matrix scaling real version (different order) More... | |
| matrix | operator/ (matrix a, nr_complex_t z) |
| Matrix scaling division by complex version. More... | |
| matrix | operator/ (matrix a, nr_double_t d) |
| Matrix scaling division by real version. More... | |
| matrix | operator* (matrix a, matrix b) |
| matrix | operator+ (matrix a, nr_complex_t z) |
| Complex scalar addition. More... | |
| matrix | operator+ (nr_complex_t z, matrix a) |
| Complex scalar addition different order. More... | |
| matrix | operator+ (matrix a, nr_double_t d) |
| Real scalar addition. More... | |
| matrix | operator+ (nr_double_t d, matrix a) |
| Real scalar addition different order. More... | |
| matrix | operator- (matrix a, nr_complex_t z) |
| Complex scalar substraction. More... | |
| matrix | operator- (nr_complex_t z, matrix a) |
| Complex scalar substraction different order. More... | |
| matrix | operator- (matrix a, nr_double_t d) |
| Real scalar substraction. More... | |
| matrix | operator- (nr_double_t d, matrix a) |
| Real scalar substraction different order. More... | |
| matrix | transpose (matrix a) |
| Matrix transposition. More... | |
| matrix | conj (matrix a) |
| Conjugate complex matrix. More... | |
| matrix | adjoint (matrix a) |
| adjoint matrix More... | |
| matrix | abs (matrix a) |
| Computes magnitude of each matrix element. More... | |
| matrix | dB (matrix a) |
| Computes magnitude in dB of each matrix element. More... | |
| matrix | arg (matrix a) |
| Computes the argument of each matrix element. More... | |
| matrix | real (matrix a) |
| Real part matrix. More... | |
| matrix | imag (matrix a) |
| Imaginary part matrix. More... | |
| matrix | sqr (matrix a) |
| Multiply a matrix by itself. More... | |
| matrix | eye (int rs, int cs) |
| Create identity matrix with specified number of rows and columns. More... | |
| matrix | eye (int s) |
| Create a square identity matrix. More... | |
| matrix | diagonal (qucs::vector diag) |
| Create a diagonal matrix from a vector. More... | |
| matrix | pow (matrix a, int n) |
| nr_complex_t | cofactor (matrix a, int u, int v) |
| Computes the complex cofactor of the given determinant. More... | |
| nr_complex_t | detLaplace (matrix a) |
| Compute determinant of the given matrix using Laplace expansion. More... | |
| nr_complex_t | detGauss (matrix a) |
| Compute determinant Gaussian algorithm. More... | |
| nr_complex_t | det (matrix a) |
| Compute determinant of the given matrix. More... | |
| matrix | inverseLaplace (matrix a) |
| Compute inverse matrix using Laplace expansion. More... | |
| matrix | inverseGaussJordan (matrix a) |
| Compute inverse matrix using Gauss-Jordan elimination. More... | |
| matrix | inverse (matrix a) |
| Compute inverse matrix. More... | |
| matrix | stos (matrix s, qucs::vector zref, qucs::vector z0) |
| S params to S params. More... | |
| matrix | stos (matrix s, nr_complex_t zref, nr_complex_t z0) |
| S renormalization with all part identic. More... | |
| matrix | stos (matrix s, nr_double_t zref, nr_double_t z0) |
| S renormalization with all part identic and real. More... | |
| matrix | stos (matrix s, qucs::vector zref, nr_complex_t z0) |
| S renormalization (variation) More... | |
| matrix | stos (matrix s, nr_complex_t zref, qucs::vector z0) |
| S renormalization (variation) More... | |
| matrix | stoz (matrix s, qucs::vector z0) |
| Scattering parameters to impedance matrix. More... | |
| matrix | stoz (matrix s, nr_complex_t z0) |
| Scattering parameters to impedance matrix identic case. More... | |
| matrix | ztos (matrix z, qucs::vector z0) |
| Convert impedance matrix scattering parameters. More... | |
| matrix | ztos (matrix z, nr_complex_t z0) |
| Convert impedance matrix to scattering parameters identic case. More... | |
| matrix | ztoy (matrix z) |
| impedance matrix to admittance matrix. More... | |
| matrix | stoy (matrix s, qucs::vector z0) |
| Scattering parameters to admittance matrix. More... | |
| matrix | stoy (matrix s, nr_complex_t z0) |
| Convert scattering pto adminttance parameters identic case. More... | |
| matrix | ytos (matrix y, qucs::vector z0) |
| Admittance matrix to scattering parameters. More... | |
| matrix | ytos (matrix y, nr_complex_t z0) |
| Convert Admittance matrix to scattering parameters identic case. More... | |
| matrix | stoa (matrix s, nr_complex_t z1, nr_complex_t z2) |
| Converts chain matrix to scattering parameters. More... | |
| matrix | atos (matrix a, nr_complex_t z1, nr_complex_t z2) |
| Converts chain matrix to scattering parameters. More... | |
| matrix | stoh (matrix s, nr_complex_t z1, nr_complex_t z2) |
| Converts scattering parameters to hybrid matrix. More... | |
| matrix | htos (matrix h, nr_complex_t z1, nr_complex_t z2) |
| Converts hybrid matrix to scattering parameters. More... | |
| matrix | stog (matrix s, nr_complex_t z1, nr_complex_t z2) |
| matrix | gtos (matrix g, nr_complex_t z1, nr_complex_t z2) |
| matrix | ytoz (matrix y) |
| Convert admittance matrix to impedance matrix. More... | |
| matrix | cytocs (matrix cy, matrix s) |
| Admittance noise correlation matrix to S-parameter noise correlation matrix. More... | |
| matrix | cstocy (matrix cs, matrix y) |
| Converts S-parameter noise correlation matrix to admittance noise correlation matrix. More... | |
| matrix | cztocs (matrix cz, matrix s) |
| Converts impedance noise correlation matrix to S-parameter noise correlation matrix. More... | |
| matrix | cstocz (matrix cs, matrix z) |
| Converts S-parameter noise correlation matrix to impedance noise correlation matrix. More... | |
| matrix | cztocy (matrix cz, matrix y) |
| Converts impedance noise correlation matrix to admittance noise correlation matrix. More... | |
| matrix | cytocz (matrix cy, matrix z) |
| Converts admittance noise correlation matrix to impedance noise correlation matrix. More... | |
| matrix | twoport (matrix m, char in, char out) |
| Generic conversion matrix. More... | |
| matrix | diagonal (vector) |
| matrix | stos (matrix, vector, nr_complex_t z0=50.0) |
| matrix | stos (matrix, nr_complex_t, vector) |
| matrix | stos (matrix, vector, vector) |
| matrix | stoz (matrix, vector) |
| matrix | ztos (matrix, vector) |
| matrix | stoy (matrix, vector) |
| matrix | ytos (matrix, vector) |
| nr_double_t | rollet (matrix) |
| nr_double_t | b1 (matrix) |
| nr_double_t | cos (const nr_double_t arg) |
| Compute cosine of an angle. More... | |
| nr_double_t | sin (const nr_double_t arg) |
| Compute sine of an angle. More... | |
| nr_double_t | tan (const nr_double_t arg) |
| Compute tangent of an angle. More... | |
| nr_double_t | acos (const nr_double_t arg) |
| Compute arc cosine. More... | |
| nr_double_t | asin (const nr_double_t arg) |
| Compute arc sine. More... | |
| nr_double_t | atan (const nr_double_t arg) |
| Compute arc tangent. More... | |
| nr_double_t | atan2 (const nr_double_t x, const nr_double_t y) |
| Compute arc tangent with two parameters (fortran like function) More... | |
| nr_double_t | cosh (const nr_double_t arg) |
| Compute hyperbolic cosine. More... | |
| nr_double_t | sinh (const nr_double_t arg) |
| Compute hyperbolic sine. More... | |
| nr_double_t | tanh (const nr_double_t arg) |
| Compute hyperbolic tangent. More... | |
| nr_double_t | acosh (const nr_double_t arg) |
| Compute arc hyperbolic cosine. More... | |
| nr_double_t | asinh (const nr_double_t arg) |
| Compute arc hyperbolic sine. More... | |
| nr_double_t | atanh (const nr_double_t arg) |
| Compute arc hyperbolic tangent. More... | |
| nr_double_t | exp (const nr_double_t arg) |
| nr_double_t | log (const nr_double_t arg) |
| nr_double_t | log10 (const nr_double_t arg) |
| nr_double_t | pow (const nr_double_t a, const nr_double_t b) |
| nr_double_t | sqrt (const nr_double_t d) |
| nr_double_t | xhypot (const nr_double_t a, const nr_double_t b) |
| Euclidean distance function. More... | |
| nr_double_t | erf (nr_double_t arg) |
| nr_double_t | ceil (nr_double_t arg) |
| nr_double_t | floor (nr_double_t arg) |
| nr_double_t | fmod (nr_double_t arg) |
| nr_double_t | trunc (nr_double_t arg) |
| nr_double_t | round (nr_double_t arg) |
| nr_double_t | coth (const nr_double_t d) |
| nr_double_t | sech (const nr_double_t d) |
| nr_double_t | cosech (const nr_double_t d) |
| nr_double_t | sqr (const nr_double_t r) |
| Square a value. More... | |
| unsigned int | sqr (unsigned int r) |
| nr_double_t | quadr (const nr_double_t r) |
| Quartic function. More... | |
| nr_double_t | limexp (const nr_double_t r) |
| Compute limited exponential. More... | |
| nr_double_t | signum (const nr_double_t d) |
| real signum function More... | |
| nr_double_t | sign (const nr_double_t d) |
| real sign function More... | |
| nr_double_t | sinc (const nr_double_t d) |
| Real cardinal sinus. More... | |
| nr_double_t | fix (const nr_double_t d) |
| Fix function. More... | |
| nr_double_t | step (const nr_double_t d) |
| Heaviside step function. More... | |
| unsigned int | factorial (unsigned int n) |
| Compute factorial n ie $n!$. More... | |
| nr_double_t | real (const nr_double_t r) |
| Real part of real number. More... | |
| nr_double_t | imag (const nr_double_t r) |
| Imaginary part of complex number. More... | |
| nr_double_t | norm (const nr_double_t r) |
| Compute euclidian norm of real number. More... | |
| nr_double_t | abs (const nr_double_t r) |
| Compute complex modulus of real number. More... | |
| nr_double_t | conj (const nr_double_t r) |
| Conjugate of real number. More... | |
| matvec | operator+ (matvec a, matvec b) |
| matvec | operator+ (matvec a, matrix b) |
| matvec | operator+ (matvec a, qucs::vector b) |
| matvec | operator+ (qucs::vector b, matvec a) |
| matvec | operator+ (matrix a, matvec b) |
| matvec | operator+ (matvec a, nr_complex_t z) |
| matvec | operator+ (nr_complex_t z, matvec a) |
| matvec | operator+ (matvec a, nr_double_t d) |
| matvec | operator+ (nr_double_t d, matvec a) |
| matvec | operator- (matvec a, nr_complex_t z) |
| matvec | operator- (nr_complex_t z, matvec a) |
| matvec | operator- (matvec a, nr_double_t d) |
| matvec | operator- (nr_double_t d, matvec a) |
| matvec | operator- (matvec a, matvec b) |
| matvec | operator- (matvec a, matrix b) |
| matvec | operator- (matrix a, matvec b) |
| matvec | operator- (matvec a, qucs::vector b) |
| matvec | operator- (qucs::vector b, matvec a) |
| matvec | operator* (matvec a, nr_complex_t z) |
| matvec | operator* (nr_complex_t z, matvec a) |
| matvec | operator* (matvec a, nr_double_t d) |
| matvec | operator* (nr_double_t d, matvec a) |
| matvec | operator* (matvec a, qucs::vector b) |
| matvec | operator* (qucs::vector a, matvec b) |
| matvec | operator/ (matvec a, nr_complex_t z) |
| matvec | operator/ (matvec a, nr_double_t d) |
| matvec | operator/ (matvec a, qucs::vector b) |
| matvec | operator* (matvec a, matvec b) |
| matvec | operator* (matvec a, matrix b) |
| matvec | operator* (matrix a, matvec b) |
| qucs::vector | det (matvec a) |
| matvec | inverse (matvec a) |
| matvec | sqr (matvec a) |
| matvec | pow (matvec a, int n) |
| matvec | pow (matvec a, qucs::vector v) |
| matvec | conj (matvec a) |
| matvec | abs (matvec a) |
| matvec | dB (matvec a) |
| matvec | arg (matvec a) |
| matvec | real (matvec a) |
| matvec | imag (matvec a) |
| matvec | adjoint (matvec a) |
| matvec | transpose (matvec a) |
| matvec | stos (matvec s, qucs::vector zref, qucs::vector z0) |
| matvec | stos (matvec s, nr_complex_t zref, nr_complex_t z0) |
| matvec | stos (matvec s, nr_double_t zref, nr_double_t z0) |
| matvec | stos (matvec s, qucs::vector zref, nr_complex_t z0) |
| matvec | stos (matvec s, nr_complex_t zref, qucs::vector z0) |
| matvec | stoy (matvec s, qucs::vector z0) |
| matvec | stoy (matvec s, nr_complex_t z0) |
| matvec | ytos (matvec y, qucs::vector z0) |
| matvec | ytos (matvec y, nr_complex_t z0) |
| matvec | stoz (matvec s, qucs::vector z0) |
| matvec | stoz (matvec s, nr_complex_t z0) |
| matvec | ztos (matvec z, qucs::vector z0) |
| matvec | ztos (matvec z, nr_complex_t z0) |
| matvec | ztoy (matvec z) |
| matvec | ytoz (matvec y) |
| matvec | twoport (matvec m, char in, char out) |
| qucs::vector | rollet (matvec m) |
| qucs::vector | b1 (matvec m) |
| matvec | pow (matvec, vector) |
| matvec | stos (matvec, vector, nr_complex_t z0=50.0) |
| matvec | stos (matvec, nr_complex_t, vector) |
| matvec | stos (matvec, vector, vector) |
| matvec | stoz (matvec, vector) |
| matvec | ztos (matvec, vector) |
| matvec | stoy (matvec, vector) |
| matvec | ytos (matvec, vector) |
| static int | sortfunc (struct nodelist_t *n) |
| static int | insfunc (struct nodelist_t *n1, struct nodelist_t *n2) |
| qucs::vector | linspace (nr_double_t, nr_double_t, int) |
| qucs::vector | logspace (nr_double_t, nr_double_t, int) |
| qucs::vector | runavg (qucs::vector, const int) |
| qucs::vector | runavg (const nr_complex_t, const int) |
| nr_complex_t | sum (vector) |
| nr_complex_t | prod (vector) |
| nr_complex_t | avg (vector) |
| vector | cumsum (vector) |
| vector | cumprod (vector) |
| vector | cumavg (vector) |
| vector | dbm (vector, const nr_complex_t z=50.0) |
| nr_complex_t | integrate (vector v, const nr_complex_t) |
| nr_double_t | integrate (vector v, const nr_double_t) |
| vector | real (vector) |
| vector | imag (vector) |
| vector | conj (vector) |
| vector | norm (vector) |
| vector | arg (vector) |
| vector | dB (vector) |
| vector | log (vector) |
| vector | log2 (vector) |
| vector | pow (vector, const nr_complex_t) |
| vector | pow (vector, const nr_double_t) |
| vector | pow (const nr_complex_t, vector) |
| vector | pow (const nr_double_t, vector) |
| vector | pow (vector, vector) |
| vector | ztor (vector, nr_complex_t zref=50.0) |
| vector | rtoz (vector, nr_complex_t zref=50.0) |
| vector | ytor (vector, nr_complex_t zref=50.0) |
| vector | rtoy (vector, nr_complex_t zref=50.0) |
| vector | diff (vector, vector, int n=1) |
| vector | unwrap (vector, nr_double_t tol=M_PI, nr_double_t step=2 *M_PI) |
| vector | polar (vector, const nr_complex_t) |
| vector | polar (const nr_complex_t, vector) |
| vector | polar (vector, vector) |
| vector | atan2 (vector, const nr_double_t) |
| vector | atan2 (const nr_double_t, vector) |
| vector | atan2 (vector, vector) |
| vector | dbm2w (vector) |
| vector | w2dbm (vector) |
| vector | xhypot (vector, vector) |
| vector | xhypot (vector, const nr_complex_t) |
| vector | xhypot (vector, const nr_double_t) |
| vector | xhypot (const nr_complex_t, vector) |
| vector | xhypot (const nr_double_t, vector) |
| vector | abs (vector) |
| vector | log10 (vector) |
| vector | exp (vector) |
| vector | limexp (vector) |
| vector | sqrt (vector) |
| vector | sin (vector) |
| vector | asin (vector) |
| vector | cos (vector) |
| vector | acos (vector) |
| vector | tan (vector) |
| vector | atan (vector) |
| vector | cot (vector) |
| vector | acot (vector) |
| vector | sinh (vector) |
| vector | asinh (vector) |
| vector | cosh (vector) |
| vector | sech (vector) |
| vector | cosech (vector) |
| vector | acosh (vector) |
| vector | asech (vector) |
| vector | tanh (vector) |
| vector | atanh (vector) |
| vector | coth (vector) |
| vector | acoth (vector) |
| vector | signum (vector) |
| vector | sign (vector) |
| vector | sinc (vector) |
| vector | ceil (vector) |
| vector | floor (vector) |
| vector | fix (vector) |
| vector | round (vector) |
| vector | sqr (vector) |
| vector | step (vector) |
| vector | jn (const int, vector) |
| vector | yn (const int, vector) |
| vector | i0 (vector) |
| vector | erf (vector) |
| vector | erfc (vector) |
| vector | erfinv (vector) |
| vector | erfcinv (vector) |
| template<class nr_type_t > | |
| tmatrix< nr_type_t > | inverse (tmatrix< nr_type_t > a) |
| template<class nr_type_t > | |
| tmatrix< nr_type_t > | teye (int n) |
| template<class nr_type_t > | |
| tmatrix< nr_type_t > | operator* (tmatrix< nr_type_t > a, tmatrix< nr_type_t > b) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator* (tmatrix< nr_type_t > a, tvector< nr_type_t > b) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator* (tvector< nr_type_t > a, tmatrix< nr_type_t > b) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator+ (tvector< nr_type_t > a, tvector< nr_type_t > b) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator- (tvector< nr_type_t > a, tvector< nr_type_t > b) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator* (nr_double_t s, tvector< nr_type_t > a) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator* (tvector< nr_type_t > a, nr_double_t s) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator* (tvector< nr_type_t > a, tvector< nr_type_t > b) |
| template<class nr_type_t > | |
| nr_type_t | scalar (tvector< nr_type_t > a, tvector< nr_type_t > b) |
| template<class nr_type_t > | |
| nr_type_t | sum (tvector< nr_type_t > a) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator- (tvector< nr_type_t > a) |
| template<class nr_type_t > | |
| bool | operator< (tvector< nr_type_t > a, tvector< nr_type_t > b) |
| template<class nr_type_t > | |
| bool | operator> (tvector< nr_type_t > a, tvector< nr_type_t > b) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator+ (nr_type_t s, tvector< nr_type_t > a) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | operator+ (tvector< nr_type_t > a, nr_type_t s) |
| template<class nr_type_t > | |
| nr_double_t | norm (tvector< nr_type_t > a) |
| template<class nr_type_t > | |
| nr_double_t | maxnorm (tvector< nr_type_t > a) |
| template<class nr_type_t > | |
| tvector< nr_type_t > | conj (tvector< nr_type_t > a) |
| vector | operator+ (vector v1, vector v2) |
| vector | operator+ (vector v, const nr_complex_t c) |
| vector | operator+ (const nr_complex_t c, vector v) |
| vector | operator+ (vector v, const nr_double_t d) |
| vector | operator+ (const nr_double_t d, vector v) |
| vector | operator- (vector v1, vector v2) |
| vector | operator- (vector v, const nr_complex_t c) |
| vector | operator- (vector v, const nr_double_t d) |
| vector | operator- (const nr_complex_t c, vector v) |
| vector | operator- (const nr_double_t d, vector v) |
| vector | operator* (vector v1, vector v2) |
| vector | operator* (vector v, const nr_complex_t c) |
| vector | operator* (vector v, const nr_double_t d) |
| vector | operator* (const nr_complex_t c, vector v) |
| vector | operator* (const nr_double_t d, vector v) |
| vector | operator/ (vector v1, vector v2) |
| vector | operator/ (vector v, const nr_complex_t c) |
| vector | operator/ (vector v, const nr_double_t d) |
| vector | operator/ (const nr_complex_t c, vector v) |
| vector | operator/ (const nr_double_t d, vector v) |
| vector | operator% (vector v, const nr_complex_t z) |
| vector | operator% (vector v, const nr_double_t d) |
| vector | operator% (const nr_complex_t z, vector v) |
| vector | operator% (const nr_double_t d, vector v) |
| vector | operator% (vector v1, vector v2) |
| static nr_double_t | integrate_n (vector v) |
| vector | runavg (vector v, const int n) |
It is prefered to add all used funcions into the qucs namespace. Doing so one is forced do think about compatibility instead of using std directly. Inline is optional at this moment
| vector qucs::abs | ( | vector | ) |
Definition at line 328 of file vector.cpp.
| nr_double_t qucs::abs | ( | const nr_double_t | r | ) |
| matvec qucs::abs | ( | matvec | a | ) |
Definition at line 514 of file matvec.cpp.
| matrix qucs::abs | ( | matrix | a | ) |
Computes magnitude of each matrix element.
| [in] | a | matrix |
add abs in place
a is const
Definition at line 531 of file matrix.cpp.
| nr_double_t qucs::acos | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::acos | ( | const nr_complex_t | z | ) |
Compute complex arc cosine.
| [in] | z | complex arc |
Definition at line 84 of file complex.cpp.
| vector qucs::acos | ( | vector | ) |
Definition at line 460 of file vector.cpp.
| nr_double_t qucs::acosh | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::acosh | ( | const nr_complex_t | z | ) |
Compute complex arc hyperbolic cosine.
| [in] | z | complex arc |
Definition at line 162 of file complex.cpp.
| vector qucs::acosh | ( | vector | ) |
Definition at line 526 of file vector.cpp.
| vector qucs::acot | ( | vector | ) |
Definition at line 490 of file vector.cpp.
| nr_complex_t qucs::acot | ( | const nr_complex_t | z | ) |
Compute complex arc cotangent.
| [in] | z | complex arc |
Definition at line 310 of file complex.cpp.
| vector qucs::acoth | ( | vector | ) |
Definition at line 556 of file vector.cpp.
| nr_complex_t qucs::acoth | ( | const nr_complex_t | z | ) |
Compute complex argument hyperbolic cotangent.
| [in] | z | complex arc |
Definition at line 332 of file complex.cpp.
| matrix qucs::adjoint | ( | matrix | a | ) |
adjoint matrix
The function returns the adjoint complex matrix. This is also called the adjugate or transpose conjugate.
| [in] | a | Matrix to transpose |
add adjoint in place
Do not lazy and avoid conj and transpose copy
a is const
Definition at line 522 of file matrix.cpp.
| matvec qucs::adjoint | ( | matvec | a | ) |
Definition at line 550 of file matvec.cpp.
| vector qucs::arg | ( | vector | ) |
Definition at line 340 of file vector.cpp.
| matvec qucs::arg | ( | matvec | a | ) |
Definition at line 528 of file matvec.cpp.
| matrix qucs::arg | ( | matrix | a | ) |
Computes the argument of each matrix element.
| [in] | a | matrix |
add arg in place
a is const
Definition at line 555 of file matrix.cpp.
| vector qucs::asech | ( | vector | ) |
Definition at line 532 of file vector.cpp.
| nr_complex_t qucs::asech | ( | const nr_complex_t | z | ) |
Compute complex argument hyperbolic secant.
| [in] | z | complex arc |
Definition at line 354 of file complex.cpp.
| nr_double_t qucs::asin | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::asin | ( | const nr_complex_t | z | ) |
Compute complex arc sine.
| [in] | z | complex arc |
Definition at line 102 of file complex.cpp.
| vector qucs::asin | ( | vector | ) |
Definition at line 454 of file vector.cpp.
| nr_double_t qucs::asinh | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::asinh | ( | const nr_complex_t | z | ) |
Compute complex arc hyperbolic sine.
| [in] | z | complex arc |
Definition at line 175 of file complex.cpp.
| vector qucs::asinh | ( | vector | ) |
Definition at line 502 of file vector.cpp.
| nr_double_t qucs::atan | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::atan | ( | const nr_complex_t | z | ) |
Compute complex arc tangent.
| [in] | z | complex arc |
Definition at line 117 of file complex.cpp.
| vector qucs::atan | ( | vector | ) |
Definition at line 478 of file vector.cpp.
| nr_double_t qucs::atan2 | ( | const nr_double_t | x, |
| const nr_double_t | y | ||
| ) |
| vector qucs::atan2 | ( | vector | , |
| const nr_double_t | |||
| ) |
Definition at line 1162 of file vector.cpp.
| vector qucs::atan2 | ( | const nr_double_t | , |
| vector | |||
| ) |
Definition at line 1155 of file vector.cpp.
| vector qucs::atan2 | ( | vector | , |
| vector | |||
| ) |
Definition at line 1169 of file vector.cpp.
| nr_complex_t qucs::atan2 | ( | const nr_complex_t | y, |
| const nr_complex_t | x | ||
| ) |
Compute complex arc tangent fortran like function.
atan2 is a two-argument function that computes the arc tangent of y / x given y and x, but with a range of ![$(-\pi;\pi]$](form_62.png)
| [in] | z | complex angle |
Definition at line 377 of file complex.cpp.
| nr_double_t qucs::atanh | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::atanh | ( | const nr_complex_t | z | ) |
Compute complex arc hyperbolic tangent.
| [in] | z | complex arc |
Definition at line 188 of file complex.cpp.
| vector qucs::atanh | ( | vector | ) |
Definition at line 544 of file vector.cpp.
| matrix qucs::atos | ( | matrix | a, |
| nr_complex_t | z1, | ||
| nr_complex_t | z2 | ||
| ) |
Converts chain matrix to scattering parameters.
Converts chain matrix to scattering parameters Formulae are given by [5] and are remembered here:
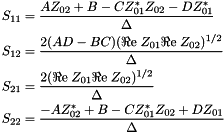
Where:
![\[ \Delta =AZ_{02}+B+CZ_{01}Z_{02}-DZ_{01} \]](form_99.png)
| [in] | a | Chain matrix |
| [in] | z1 | impedance at input 1 |
| [in] | z2 | impedance at input 2 |
Definition at line 1222 of file matrix.cpp.
| nr_complex_t qucs::avg | ( | vector | ) |
Definition at line 263 of file vector.cpp.
| nr_double_t qucs::b1 | ( | matrix | ) |
| qucs::vector qucs::b1 | ( | matvec | m | ) |
Definition at line 677 of file matvec.cpp.
| nr_complex_t qucs::cbesselj | ( | unsigned int | n, |
| nr_complex_t | z | ||
| ) |
Main entry point for besselj function.
Definition at line 287 of file complex.cpp.
|
static |
|
static |
Definition at line 201 of file complex.cpp.
|
static |
Definition at line 173 of file complex.cpp.
|
static |
Definition at line 146 of file complex.cpp.
|
static |
\param[in] n order \param[in] arg arguments
Definition at line 106 of file complex.cpp.
| vector qucs::ceil | ( | vector | ) |
Definition at line 1022 of file vector.cpp.
| nr_complex_t qucs::ceil | ( | const nr_complex_t | z | ) |
Complex ceil Ceil is the smallest integral value not less than argument Apply ceil to real and imaginary part.
| [in] | z | complex number |
Definition at line 634 of file complex.cpp.
| nr_complex_t qucs::cofactor | ( | matrix | a, |
| int | u, | ||
| int | v | ||
| ) |
Computes the complex cofactor of the given determinant.
The cofactor is the determinant obtained by deleting the row and column of a given element of a matrix or determinant. The cofactor is preceded by a + or - sign depending of the sign of 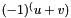
((u + v) & 1) is cryptic use (u + v)% 2
#ifdef 0
static?
Definition at line 657 of file matrix.cpp.
|
inline |
Definition at line 869 of file eqnsys.cpp.
|
inline |
Definition at line 874 of file eqnsys.cpp.
| vector qucs::conj | ( | vector | ) |
Definition at line 358 of file vector.cpp.
| tvector<nr_type_t> qucs::conj | ( | tvector< nr_type_t > | a | ) |
Definition at line 398 of file tvector.cpp.
| matrix qucs::conj | ( | matrix | a | ) |
Conjugate complex matrix.
| [in] | a | Matrix to conjugate |
add conj in place
a is const
Definition at line 505 of file matrix.cpp.
| nr_double_t qucs::conj | ( | const nr_double_t | r | ) |
| matvec qucs::conj | ( | matvec | a | ) |
Definition at line 507 of file matvec.cpp.
| nr_double_t qucs::cos | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::cos | ( | const nr_complex_t | z | ) |
Compute complex cosine.
| [in] | z | complex angle |
Definition at line 57 of file complex.cpp.
| vector qucs::cos | ( | vector | ) |
Definition at line 466 of file vector.cpp.
| vector qucs::cosech | ( | vector | ) |
Definition at line 520 of file vector.cpp.
| nr_complex_t qucs::cosech | ( | const nr_complex_t | z | ) |
Compute complex argument hyperbolic cosec.
| [in] | z | complex arc |
Definition at line 364 of file complex.cpp.
| nr_double_t qucs::cosh | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::cosh | ( | const nr_complex_t | z | ) |
Compute complex hyperbolic cosine.
| [in] | z | complex arc |
Definition at line 135 of file complex.cpp.
| vector qucs::cosh | ( | vector | ) |
Definition at line 508 of file vector.cpp.
| vector qucs::cot | ( | vector | ) |
Definition at line 484 of file vector.cpp.
| nr_complex_t qucs::cot | ( | const nr_complex_t | z | ) |
Compute complex cotangent.
| [in] | z | complex angle |
Definition at line 298 of file complex.cpp.
| vector qucs::coth | ( | vector | ) |
Definition at line 550 of file vector.cpp.
| nr_complex_t qucs::coth | ( | const nr_complex_t | z | ) |
Compute complex hyperbolic cotangent.
| [in] | z | complex angle |
Definition at line 320 of file complex.cpp.
|
static |
Definition at line 163 of file equation.cpp.
| matrix qucs::cstocy | ( | matrix | cs, |
| matrix | y | ||
| ) |
Converts S-parameter noise correlation matrix to admittance noise correlation matrix.
According to [7] fig 2:
![\[ C_y=(I+Y)C_s(I+Y)^+ \]](form_110.png)
Where  is the scattering noise correlation matrix,
is the scattering noise correlation matrix, 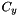 the admittance noise correlation matrix,
the admittance noise correlation matrix, 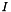 the identity matrix and
the identity matrix and 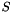 the scattering matrix of device.
the scattering matrix of device. 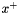 is the adjoint of
is the adjoint of 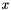
| [in] | cs | S parameter noise correlation |
| [in] | y | Admittance matrix of device |
Definition at line 1430 of file matrix.cpp.
| matrix qucs::cstocz | ( | matrix | cs, |
| matrix | z | ||
| ) |
Converts S-parameter noise correlation matrix to impedance noise correlation matrix.
According to [7] fig 2:
![\[ C_z=(I+Z)C_s(I+Z)^+ \]](form_113.png)
Where 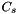 is the scattering noise correlation matrix,
is the scattering noise correlation matrix, 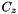 the impedance noise correlation matrix,
the impedance noise correlation matrix, 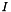 the identity matrix and
the identity matrix and 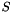 the scattering matrix of device.
the scattering matrix of device. 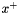 is the adjoint of
is the adjoint of 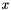
| [in] | cs | S parameter noise correlation |
| [in] | z | Impedance matrix of device |
Definition at line 1483 of file matrix.cpp.
| vector qucs::cumavg | ( | vector | ) |
Definition at line 1002 of file vector.cpp.
| vector qucs::cumprod | ( | vector | ) |
Definition at line 1012 of file vector.cpp.
| vector qucs::cumsum | ( | vector | ) |
Definition at line 992 of file vector.cpp.
| matrix qucs::cytocs | ( | matrix | cy, |
| matrix | s | ||
| ) |
Admittance noise correlation matrix to S-parameter noise correlation matrix.
Converts admittance noise correlation matrix to S-parameter noise correlation matrix. According to [7] fig 2:
![\[ C_s=\frac{1}{4}(I+S)C_y(I+S)^+ \]](form_106.png)
Where 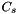 is the scattering noise correlation matrix,
is the scattering noise correlation matrix, 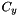 the admittance noise correlation matrix,
the admittance noise correlation matrix, 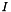 the identity matrix and
the identity matrix and 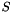 the scattering matrix of device.
the scattering matrix of device. 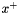 is the adjoint of
is the adjoint of 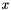
| [in] | cy | Admittance noise correlation |
| [in] | s | S parameter matrix of device |
Definition at line 1404 of file matrix.cpp.
| matrix qucs::cytocz | ( | matrix | cy, |
| matrix | z | ||
| ) |
Converts admittance noise correlation matrix to impedance noise correlation matrix.
According to [7] fig 2:
![\[ C_z=ZC_yZ^+ \]](form_115.png)
Where 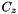 is the impedance correlation matrix,
is the impedance correlation matrix, 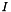 the identity matrix and
the identity matrix and 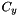 the admittance noise correlation matrix.
the admittance noise correlation matrix. 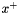 is the adjoint of
is the adjoint of 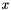
| [in] | cy | Admittance noise correlation |
| [in] | z | Impedance matrix of device |
Definition at line 1531 of file matrix.cpp.
| matrix qucs::cztocs | ( | matrix | cz, |
| matrix | s | ||
| ) |
Converts impedance noise correlation matrix to S-parameter noise correlation matrix.
According to [7] fig 2:
![\[ C_s=\frac{1}{4}(I-S)C_z(I-S) \]](form_111.png)
Where 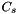 is the scattering noise correlation matrix,
is the scattering noise correlation matrix, 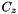 the impedance noise correlation matrix,
the impedance noise correlation matrix, 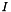 the identity matrix and
the identity matrix and 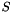 the scattering matrix of device.
the scattering matrix of device. 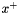 is the adjoint of
is the adjoint of 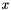
| [in] | cz | Impedance noise correlation |
| [in] | s | S parameter matrix of device |
Definition at line 1457 of file matrix.cpp.
| matrix qucs::cztocy | ( | matrix | cz, |
| matrix | y | ||
| ) |
Converts impedance noise correlation matrix to admittance noise correlation matrix.
According to [7] fig 2:
![\[ C_y=YC_zY^+ \]](form_114.png)
Where 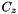 is the impedance correlation matrix,
is the impedance correlation matrix,  the identity matrix and
the identity matrix and 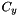 the admittance noise correlation matrix.
the admittance noise correlation matrix. 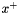 is the adjoint of
is the adjoint of 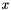
| [in] | cz | impedance noise correlation |
| [in] | y | Admittance matrix of device |
Definition at line 1507 of file matrix.cpp.
| vector qucs::dB | ( | vector | ) |
Definition at line 364 of file vector.cpp.
| matvec qucs::dB | ( | matvec | a | ) |
Definition at line 521 of file matvec.cpp.
| nr_double_t qucs::dB | ( | const nr_complex_t | z | ) |
Magnitude in dB Compute 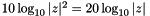 .
.
| [in] | z | complex number |
Definition at line 528 of file complex.cpp.
| matrix qucs::dB | ( | matrix | a | ) |
Computes magnitude in dB of each matrix element.
| [in] | a | matrix |
Definition at line 542 of file matrix.cpp.
| vector qucs::dbm | ( | vector | , |
| const nr_complex_t | z = 50.0 |
||
| ) |
Definition at line 1215 of file vector.cpp.
| vector qucs::dbm2w | ( | vector | ) |
Definition at line 1193 of file vector.cpp.
| qucs::vector qucs::det | ( | matvec | a | ) |
Definition at line 472 of file matvec.cpp.
| nr_complex_t qucs::det | ( | matrix | a | ) |
Compute determinant of the given matrix.
| [in] | a | matrix |
Definition at line 762 of file matrix.cpp.
| nr_complex_t qucs::detGauss | ( | matrix | a | ) |
Compute determinant Gaussian algorithm.
Compute determinant of the given matrix using the Gaussian algorithm. This means to triangulate the matrix and multiply all the diagonal elements.
| [in] | a | matrix |
static ?
a const?
Definition at line 717 of file matrix.cpp.
| nr_complex_t qucs::detLaplace | ( | matrix | a | ) |
Compute determinant of the given matrix using Laplace expansion.
The Laplace expansion of the determinant of an n by n square matrix a expresses the determinant of a as a sum of n determinants of (n-1) by (n-1) sub-matrices of a. There are 2n such expressions, one for each row and column of a.
See Wikipedia http://en.wikipedia.org/wiki/Laplace_expansion
| [in] | a | matrix |
#ifdef 0
static ?
Definition at line 686 of file matrix.cpp.
| matrix qucs::diagonal | ( | vector | ) |
| matrix qucs::diagonal | ( | qucs::vector | diag | ) |
Create a diagonal matrix from a vector.
| [in] | diag | vector to write on the diagonal |
Definition at line 624 of file matrix.cpp.
| vector qucs::diff | ( | vector | , |
| vector | , | ||
| int | n = 1 |
||
| ) |
Definition at line 591 of file vector.cpp.
| vector qucs::erf | ( | vector | ) |
Definition at line 1084 of file vector.cpp.
| nr_complex_t qucs::erf | ( | const nr_complex_t | z | ) |
Error function.
| [in] | z | argument |
Definition at line 766 of file complex.cpp.
| vector qucs::erfc | ( | vector | ) |
Definition at line 1090 of file vector.cpp.
| nr_complex_t qucs::erfc | ( | const nr_complex_t | z | ) |
Complementart error function.
| [in] | z | argument |
Definition at line 784 of file complex.cpp.
| vector qucs::erfcinv | ( | vector | ) |
Definition at line 1102 of file vector.cpp.
| nr_complex_t qucs::erfcinv | ( | const nr_complex_t | z | ) |
Inverse of complementart error function.
| [in] | z | argument |
Definition at line 813 of file complex.cpp.
| vector qucs::erfinv | ( | vector | ) |
Definition at line 1096 of file vector.cpp.
| nr_complex_t qucs::erfinv | ( | const nr_complex_t | z | ) |
Inverse of error function.
| [in] | z | argument |
Definition at line 802 of file complex.cpp.
|
static |
Helper function for the euclidian norm calculators.
Definition at line 828 of file eqnsys.cpp.
| nr_complex_t qucs::exp | ( | const nr_complex_t | z | ) |
Compute complex exponential.
| [in] | z | complex number |
Definition at line 205 of file complex.cpp.
| vector qucs::exp | ( | vector | ) |
Definition at line 377 of file vector.cpp.
Create identity matrix with specified number of rows and columns.
| [in] | rs | row number |
| [in] | cs | column number |
Avoid res.get*
Use memset
rs, cs are const
Definition at line 603 of file matrix.cpp.
| matrix qucs::eye | ( | int | s | ) |
Create a square identity matrix.
| [in] | s | row or column number of square matrix |
Do not by lazy and implement it
s is const
Definition at line 616 of file matrix.cpp.
| vector qucs::fix | ( | vector | ) |
Definition at line 1028 of file vector.cpp.
| nr_double_t qucs::fix | ( | const nr_double_t | d | ) |
| nr_complex_t qucs::fix | ( | const nr_complex_t | z | ) |
Complex fix.
Apply fix to real and imaginary part
| [in] | z | complex number |
Definition at line 645 of file complex.cpp.
| vector qucs::floor | ( | vector | ) |
Definition at line 1034 of file vector.cpp.
| nr_complex_t qucs::floor | ( | const nr_complex_t | z | ) |
Complex floor.
floor is the largest integral value not greater than argument Apply floor to real and imaginary part
| [in] | z | complex number |
Definition at line 623 of file complex.cpp.
| nr_complex_t qucs::fmod | ( | const nr_complex_t | x, |
| const nr_complex_t | y | ||
| ) |
Complex fmod Apply fmod to the complex z.
| [in] | x | complex number (numerator) |
| [in] | y | complex number (denominator) |
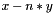 where n is the quotient of
where n is the quotient of  , rounded towards zero to an integer.
, rounded towards zero to an integer.Definition at line 662 of file complex.cpp.
|
static |
Helper function computes Givens rotation.
Definition at line 1337 of file eqnsys.cpp.
| matrix qucs::gtos | ( | matrix | g, |
| nr_complex_t | z1, | ||
| nr_complex_t | z2 | ||
| ) |
Definition at line 1355 of file matrix.cpp.
| matrix qucs::htos | ( | matrix | h, |
| nr_complex_t | z1, | ||
| nr_complex_t | z2 | ||
| ) |
Converts hybrid matrix to scattering parameters.
Formulae are given by [5] and are remembered here:
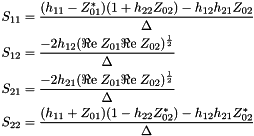
Where  is:
is:
![\[ \Delta=(Z_{01}+h_{11})(1+h_{22}Z_{02})-h_{12}h_{21}Z_{02} \]](form_104.png)
| [in] | h | hybrid matrix |
| [in] | z1 | impedance at input 1 |
| [in] | z2 | impedance at input 2 |
Definition at line 1307 of file matrix.cpp.
| vector qucs::i0 | ( | vector | ) |
Definition at line 1108 of file vector.cpp.
| nr_complex_t qucs::i0 | ( | const nr_complex_t | z | ) |
Modified Bessel function of first kind.
| [in] | z | argument |
Definition at line 754 of file complex.cpp.
| vector qucs::imag | ( | vector | ) |
Definition at line 352 of file vector.cpp.
| nr_double_t qucs::imag | ( | const nr_double_t | r | ) |
| matvec qucs::imag | ( | matvec | a | ) |
Definition at line 542 of file matvec.cpp.
| matrix qucs::imag | ( | matrix | a | ) |
Imaginary part matrix.
| [in] | a | matrix |
add imag in place
a is const
Definition at line 581 of file matrix.cpp.
|
static |
Definition at line 349 of file nodelist.cpp.
| nr_complex_t qucs::integrate | ( | vector | v, |
| const nr_complex_t | |||
| ) |
Definition at line 1207 of file vector.cpp.
| nr_double_t qucs::integrate | ( | vector | v, |
| const nr_double_t | |||
| ) |
Definition at line 1200 of file vector.cpp.
|
static |
Definition at line 1058 of file vector.cpp.
| tmatrix<nr_type_t> qucs::inverse | ( | tmatrix< nr_type_t > | a | ) |
Definition at line 197 of file tmatrix.cpp.
| matvec qucs::inverse | ( | matvec | a | ) |
Definition at line 479 of file matvec.cpp.
| matrix qucs::inverse | ( | matrix | a | ) |
Compute inverse matrix.
| [in] | a | matrix to invert |
Definition at line 847 of file matrix.cpp.
| matrix qucs::inverseGaussJordan | ( | matrix | a | ) |
Compute inverse matrix using Gauss-Jordan elimination.
Compute inverse matrix of the given matrix by Gauss-Jordan elimination.
a const?
static?
| [in] | a | matrix to invert |
Definition at line 798 of file matrix.cpp.
| matrix qucs::inverseLaplace | ( | matrix | a | ) |
Compute inverse matrix using Laplace expansion.
Compute inverse matrix of the given matrix using Laplace expansion.
| [in] | a | matrix to invert |
Static?
#ifdef 0
Definition at line 779 of file matrix.cpp.
| vector qucs::jn | ( | const int | , |
| vector | |||
| ) |
Definition at line 1114 of file vector.cpp.
| nr_complex_t qucs::jn | ( | const int | n, |
| const nr_complex_t | z | ||
| ) |
Bessel function of first kind.
| [in] | n | order |
| [in] | z | argument |
Definition at line 729 of file complex.cpp.
| vector qucs::limexp | ( | vector | ) |
Definition at line 383 of file vector.cpp.
| nr_double_t qucs::limexp | ( | const nr_double_t | r | ) |
| nr_complex_t qucs::limexp | ( | const nr_complex_t | z | ) |
Compute limited complex exponential.
| [in] | z | complex number |
Definition at line 539 of file complex.cpp.
| qucs::vector qucs::linspace | ( | nr_double_t | , |
| nr_double_t | , | ||
| int | |||
| ) |
Definition at line 950 of file vector.cpp.
| nr_complex_t qucs::log | ( | const nr_complex_t | z | ) |
Compute principal value of natural logarithm of z.
| [in] | z | complex number |
Definition at line 215 of file complex.cpp.
| vector qucs::log | ( | vector | ) |
Definition at line 389 of file vector.cpp.
| nr_complex_t qucs::log10 | ( | const nr_complex_t | z | ) |
Compute principal value of decimal logarithm of z.
| [in] | z | complex number |
Definition at line 225 of file complex.cpp.
| vector qucs::log10 | ( | vector | ) |
Definition at line 395 of file vector.cpp.
| vector qucs::log2 | ( | vector | ) |
Definition at line 401 of file vector.cpp.
| nr_complex_t qucs::log2 | ( | const nr_complex_t | z | ) |
Compute principal value of binary logarithm of z.
| [in] | z | complex number |
Definition at line 393 of file complex.cpp.
| qucs::vector qucs::logspace | ( | nr_double_t | , |
| nr_double_t | , | ||
| int | |||
| ) |
Definition at line 965 of file vector.cpp.
| nr_double_t qucs::maxnorm | ( | tvector< nr_type_t > | a | ) |
Definition at line 387 of file tvector.cpp.
| vector qucs::norm | ( | vector | ) |
Definition at line 334 of file vector.cpp.
| nr_double_t qucs::norm | ( | const nr_complex_t | z | ) |
Compute euclidian norm of complex number.
Compute 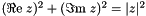
| [in] | z | Complex number |
Definition at line 283 of file complex.cpp.
| nr_double_t qucs::norm | ( | tvector< nr_type_t > | a | ) |
Definition at line 348 of file tvector.cpp.
| nr_double_t qucs::norm | ( | const nr_double_t | r | ) |
| bool qucs::operator!= | ( | const nr_complex_t | z1, |
| const nr_complex_t | z2 | ||
| ) |
Inequality of two complex.
Definition at line 865 of file complex.cpp.
| nr_complex_t qucs::operator% | ( | const nr_complex_t | z1, |
| const nr_complex_t | z2 | ||
| ) |
| nr_complex_t qucs::operator% | ( | const nr_complex_t | z1, |
| const nr_double_t | r2 | ||
| ) |
| nr_complex_t qucs::operator% | ( | const nr_double_t | r1, |
| const nr_complex_t | z2 | ||
| ) |
| vector qucs::operator% | ( | vector | v, |
| const nr_complex_t | z | ||
| ) |
Definition at line 857 of file vector.cpp.
| vector qucs::operator% | ( | vector | v, |
| const nr_double_t | d | ||
| ) |
Definition at line 864 of file vector.cpp.
| vector qucs::operator% | ( | const nr_complex_t | z, |
| vector | v | ||
| ) |
Definition at line 871 of file vector.cpp.
| vector qucs::operator% | ( | const nr_double_t | d, |
| vector | v | ||
| ) |
Definition at line 878 of file vector.cpp.
| vector qucs::operator% | ( | vector | v1, |
| vector | v2 | ||
| ) |
Definition at line 885 of file vector.cpp.
| tvector<nr_type_t> qucs::operator* | ( | nr_double_t | s, |
| tvector< nr_type_t > | a | ||
| ) |
Definition at line 259 of file tvector.cpp.
| tvector<nr_type_t> qucs::operator* | ( | tvector< nr_type_t > | a, |
| nr_double_t | s | ||
| ) |
Definition at line 267 of file tvector.cpp.
| tvector<nr_type_t> qucs::operator* | ( | tvector< nr_type_t > | a, |
| tvector< nr_type_t > | b | ||
| ) |
Definition at line 273 of file tvector.cpp.
| tmatrix<nr_type_t> qucs::operator* | ( | tmatrix< nr_type_t > | a, |
| tmatrix< nr_type_t > | b | ||
| ) |
Definition at line 275 of file tmatrix.cpp.
| tvector<nr_type_t> qucs::operator* | ( | tmatrix< nr_type_t > | a, |
| tvector< nr_type_t > | b | ||
| ) |
Definition at line 291 of file tmatrix.cpp.
| matrix qucs::operator* | ( | matrix | a, |
| nr_complex_t | z | ||
| ) |
Matrix scaling complex version.
| [in] | a | matrix to scale |
| [in] | z | scaling complex |
Definition at line 298 of file matrix.cpp.
| tvector<nr_type_t> qucs::operator* | ( | tvector< nr_type_t > | a, |
| tmatrix< nr_type_t > | b | ||
| ) |
Definition at line 306 of file tmatrix.cpp.
| matrix qucs::operator* | ( | nr_complex_t | z, |
| matrix | a | ||
| ) |
Matrix scaling complex version (different order)
| [in] | a | matrix to scale |
| [in] | z | scaling complex |
Why not a and z const
Why not inline
Definition at line 313 of file matrix.cpp.
| matrix qucs::operator* | ( | matrix | a, |
| nr_double_t | d | ||
| ) |
Matrix scaling complex version.
| [in] | a | matrix to scale |
| [in] | d | scaling real |
Definition at line 323 of file matrix.cpp.
| matrix qucs::operator* | ( | nr_double_t | d, |
| matrix | a | ||
| ) |
Matrix scaling real version (different order)
| [in] | a | matrix to scale |
| [in] | d | scaling real |
Why not inline?
Why not d and a const
Definition at line 338 of file matrix.cpp.
| matrix qucs::operator* | ( | matrix | a, |
| matrix | b | ||
| ) |
Matrix multiplication.
Dumb and not optimized matrix multiplication
| a] | first matrix |
| b] | second matrix |
Definition at line 378 of file matrix.cpp.
| matvec qucs::operator* | ( | matvec | a, |
| nr_complex_t | z | ||
| ) |
Definition at line 392 of file matvec.cpp.
| matvec qucs::operator* | ( | nr_complex_t | z, |
| matvec | a | ||
| ) |
Definition at line 399 of file matvec.cpp.
| matvec qucs::operator* | ( | matvec | a, |
| nr_double_t | d | ||
| ) |
Definition at line 404 of file matvec.cpp.
| matvec qucs::operator* | ( | nr_double_t | d, |
| matvec | a | ||
| ) |
Definition at line 411 of file matvec.cpp.
| matvec qucs::operator* | ( | matvec | a, |
| qucs::vector | b | ||
| ) |
Definition at line 416 of file matvec.cpp.
| matvec qucs::operator* | ( | qucs::vector | a, |
| matvec | b | ||
| ) |
Definition at line 424 of file matvec.cpp.
| matvec qucs::operator* | ( | matvec | a, |
| matvec | b | ||
| ) |
Definition at line 451 of file matvec.cpp.
| matvec qucs::operator* | ( | matvec | a, |
| matrix | b | ||
| ) |
Definition at line 459 of file matvec.cpp.
| matvec qucs::operator* | ( | matrix | a, |
| matvec | b | ||
| ) |
Definition at line 467 of file matvec.cpp.
| vector qucs::operator* | ( | vector | v1, |
| vector | v2 | ||
| ) |
Definition at line 766 of file vector.cpp.
| vector qucs::operator* | ( | vector | v, |
| const nr_complex_t | c | ||
| ) |
Definition at line 779 of file vector.cpp.
| vector qucs::operator* | ( | vector | v, |
| const nr_double_t | d | ||
| ) |
Definition at line 785 of file vector.cpp.
| vector qucs::operator* | ( | const nr_complex_t | c, |
| vector | v | ||
| ) |
Definition at line 791 of file vector.cpp.
| vector qucs::operator* | ( | const nr_double_t | d, |
| vector | v | ||
| ) |
Definition at line 795 of file vector.cpp.
| tvector<nr_type_t> qucs::operator+ | ( | tvector< nr_type_t > | a, |
| tvector< nr_type_t > | b | ||
| ) |
Definition at line 203 of file tvector.cpp.
| matrix qucs::operator+ | ( | matrix | a, |
| matrix | b | ||
| ) |
Matrix addition.
| a] | first matrix |
| b] | second matrix |
Definition at line 228 of file matrix.cpp.
| matvec qucs::operator+ | ( | matvec | a, |
| matvec | b | ||
| ) |
Definition at line 246 of file matvec.cpp.
| matvec qucs::operator+ | ( | matvec | a, |
| matrix | b | ||
| ) |
Definition at line 255 of file matvec.cpp.
| matvec qucs::operator+ | ( | matvec | a, |
| qucs::vector | b | ||
| ) |
Definition at line 263 of file matvec.cpp.
| matvec qucs::operator+ | ( | qucs::vector | b, |
| matvec | a | ||
| ) |
Definition at line 271 of file matvec.cpp.
| matvec qucs::operator+ | ( | matrix | a, |
| matvec | b | ||
| ) |
Definition at line 276 of file matvec.cpp.
| matvec qucs::operator+ | ( | matvec | a, |
| nr_complex_t | z | ||
| ) |
Definition at line 281 of file matvec.cpp.
| matvec qucs::operator+ | ( | nr_complex_t | z, |
| matvec | a | ||
| ) |
Definition at line 288 of file matvec.cpp.
| matvec qucs::operator+ | ( | matvec | a, |
| nr_double_t | d | ||
| ) |
Definition at line 295 of file matvec.cpp.
| matvec qucs::operator+ | ( | nr_double_t | d, |
| matvec | a | ||
| ) |
Definition at line 302 of file matvec.cpp.
| tvector<nr_type_t> qucs::operator+ | ( | nr_type_t | s, |
| tvector< nr_type_t > | a | ||
| ) |
Definition at line 334 of file tvector.cpp.
| tvector<nr_type_t> qucs::operator+ | ( | tvector< nr_type_t > | a, |
| nr_type_t | s | ||
| ) |
Definition at line 342 of file tvector.cpp.
| matrix qucs::operator+ | ( | matrix | a, |
| nr_complex_t | z | ||
| ) |
Complex scalar addition.
| [in] | a | matrix |
| [in] | z | complex to add |
Move near other +
a and z are const
Definition at line 399 of file matrix.cpp.
| matrix qucs::operator+ | ( | nr_complex_t | z, |
| matrix | a | ||
| ) |
Complex scalar addition different order.
| [in] | a | matrix |
| [in] | z | complex to add |
Move near other +
a and z are const
Why not inline
Definition at line 414 of file matrix.cpp.
| matrix qucs::operator+ | ( | matrix | a, |
| nr_double_t | d | ||
| ) |
Real scalar addition.
| [in] | a | matrix |
| [in] | d | real to add |
Move near other +
a and d are const
Definition at line 424 of file matrix.cpp.
| matrix qucs::operator+ | ( | nr_double_t | d, |
| matrix | a | ||
| ) |
Real scalar addition different order.
| [in] | a | matrix |
| [in] | d | real to add |
Move near other +
a and d are const
Why not inline
Definition at line 439 of file matrix.cpp.
| vector qucs::operator+ | ( | vector | v1, |
| vector | v2 | ||
| ) |
Definition at line 656 of file vector.cpp.
| vector qucs::operator+ | ( | vector | v, |
| const nr_complex_t | c | ||
| ) |
Definition at line 669 of file vector.cpp.
| vector qucs::operator+ | ( | const nr_complex_t | c, |
| vector | v | ||
| ) |
Definition at line 675 of file vector.cpp.
| vector qucs::operator+ | ( | vector | v, |
| const nr_double_t | d | ||
| ) |
Definition at line 679 of file vector.cpp.
| vector qucs::operator+ | ( | const nr_double_t | d, |
| vector | v | ||
| ) |
Definition at line 685 of file vector.cpp.
| tvector<nr_type_t> qucs::operator- | ( | tvector< nr_type_t > | a, |
| tvector< nr_type_t > | b | ||
| ) |
Definition at line 223 of file tvector.cpp.
| matrix qucs::operator- | ( | matrix | a, |
| matrix | b | ||
| ) |
Matrix subtraction.
| a] | first matrix |
| b] | second matrix |
Definition at line 259 of file matrix.cpp.
| tvector<nr_type_t> qucs::operator- | ( | tvector< nr_type_t > | a | ) |
Definition at line 307 of file tvector.cpp.
| matvec qucs::operator- | ( | matvec | a, |
| nr_complex_t | z | ||
| ) |
Definition at line 309 of file matvec.cpp.
| matvec qucs::operator- | ( | nr_complex_t | z, |
| matvec | a | ||
| ) |
Definition at line 316 of file matvec.cpp.
| matvec qucs::operator- | ( | matvec | a, |
| nr_double_t | d | ||
| ) |
Definition at line 323 of file matvec.cpp.
| matvec qucs::operator- | ( | nr_double_t | d, |
| matvec | a | ||
| ) |
Definition at line 330 of file matvec.cpp.
| matvec qucs::operator- | ( | matvec | a, |
| matvec | b | ||
| ) |
Definition at line 345 of file matvec.cpp.
| matvec qucs::operator- | ( | matvec | a, |
| matrix | b | ||
| ) |
Definition at line 354 of file matvec.cpp.
| matvec qucs::operator- | ( | matrix | a, |
| matvec | b | ||
| ) |
Definition at line 362 of file matvec.cpp.
| matvec qucs::operator- | ( | matvec | a, |
| qucs::vector | b | ||
| ) |
Definition at line 367 of file matvec.cpp.
| matvec qucs::operator- | ( | qucs::vector | b, |
| matvec | a | ||
| ) |
Definition at line 372 of file matvec.cpp.
| matrix qucs::operator- | ( | matrix | a, |
| nr_complex_t | z | ||
| ) |
Complex scalar substraction.
| [in] | a | matrix |
| [in] | z | complex to add |
Move near other +
a and z are const
Why not inline
Definition at line 450 of file matrix.cpp.
| matrix qucs::operator- | ( | nr_complex_t | z, |
| matrix | a | ||
| ) |
Complex scalar substraction different order.
| [in] | a | matrix |
| [in] | z | complex to add |
Move near other +
a and z are const
Why not inline
Definition at line 461 of file matrix.cpp.
| matrix qucs::operator- | ( | matrix | a, |
| nr_double_t | d | ||
| ) |
Real scalar substraction.
| [in] | a | matrix |
| [in] | z | real to add |
Move near other +
a and z are const
Why not inline
Definition at line 472 of file matrix.cpp.
| matrix qucs::operator- | ( | nr_double_t | d, |
| matrix | a | ||
| ) |
Real scalar substraction different order.
| [in] | a | matrix |
| [in] | z | real to add |
Move near other +
a and z are const
Why not inline
Definition at line 483 of file matrix.cpp.
| vector qucs::operator- | ( | vector | v1, |
| vector | v2 | ||
| ) |
Definition at line 712 of file vector.cpp.
| vector qucs::operator- | ( | vector | v, |
| const nr_complex_t | c | ||
| ) |
Definition at line 725 of file vector.cpp.
| vector qucs::operator- | ( | vector | v, |
| const nr_double_t | d | ||
| ) |
Definition at line 731 of file vector.cpp.
| vector qucs::operator- | ( | const nr_complex_t | c, |
| vector | v | ||
| ) |
Definition at line 737 of file vector.cpp.
| vector qucs::operator- | ( | const nr_double_t | d, |
| vector | v | ||
| ) |
Definition at line 743 of file vector.cpp.
| matrix qucs::operator/ | ( | matrix | a, |
| nr_complex_t | z | ||
| ) |
Matrix scaling division by complex version.
| [in] | a | matrix to scale |
| [in] | z | scaling complex |
Definition at line 348 of file matrix.cpp.
| matrix qucs::operator/ | ( | matrix | a, |
| nr_double_t | d | ||
| ) |
Matrix scaling division by real version.
| [in] | a | matrix to scale |
| [in] | d | scaling real |
Definition at line 362 of file matrix.cpp.
| matvec qucs::operator/ | ( | matvec | a, |
| nr_complex_t | z | ||
| ) |
Definition at line 429 of file matvec.cpp.
| matvec qucs::operator/ | ( | matvec | a, |
| nr_double_t | d | ||
| ) |
Definition at line 436 of file matvec.cpp.
| matvec qucs::operator/ | ( | matvec | a, |
| qucs::vector | b | ||
| ) |
Definition at line 443 of file matvec.cpp.
| vector qucs::operator/ | ( | vector | v1, |
| vector | v2 | ||
| ) |
Definition at line 816 of file vector.cpp.
| vector qucs::operator/ | ( | vector | v, |
| const nr_complex_t | c | ||
| ) |
Definition at line 831 of file vector.cpp.
| vector qucs::operator/ | ( | vector | v, |
| const nr_double_t | d | ||
| ) |
Definition at line 837 of file vector.cpp.
| vector qucs::operator/ | ( | const nr_complex_t | c, |
| vector | v | ||
| ) |
Definition at line 843 of file vector.cpp.
| vector qucs::operator/ | ( | const nr_double_t | d, |
| vector | v | ||
| ) |
Definition at line 850 of file vector.cpp.
| bool qucs::operator< | ( | tvector< nr_type_t > | a, |
| tvector< nr_type_t > | b | ||
| ) |
Definition at line 316 of file tvector.cpp.
| bool qucs::operator< | ( | const nr_complex_t | z1, |
| const nr_complex_t | z2 | ||
| ) |
| bool qucs::operator<= | ( | const nr_complex_t | z1, |
| const nr_complex_t | z2 | ||
| ) |
| bool qucs::operator== | ( | const nr_complex_t | z1, |
| const nr_complex_t | z2 | ||
| ) |
Equality of two complex.
Definition at line 854 of file complex.cpp.
| bool qucs::operator> | ( | tvector< nr_type_t > | a, |
| tvector< nr_type_t > | b | ||
| ) |
Definition at line 325 of file tvector.cpp.
| bool qucs::operator> | ( | const nr_complex_t | z1, |
| const nr_complex_t | z2 | ||
| ) |
| bool qucs::operator>= | ( | const nr_complex_t | z1, |
| const nr_complex_t | z2 | ||
| ) |
| vector qucs::polar | ( | vector | , |
| const nr_complex_t | |||
| ) |
Definition at line 1132 of file vector.cpp.
| vector qucs::polar | ( | const nr_complex_t | , |
| vector | |||
| ) |
Definition at line 1126 of file vector.cpp.
| vector qucs::polar | ( | vector | , |
| vector | |||
| ) |
Definition at line 1138 of file vector.cpp.
| nr_complex_t qucs::polar | ( | const nr_double_t | mag, |
| const nr_double_t | ang | ||
| ) |
Construct a complex number using polar notation.
| [in] | mag | Magnitude |
| [in] | ang | Angle |
Definition at line 551 of file complex.cpp.
| nr_complex_t qucs::polar | ( | const nr_complex_t | a, |
| const nr_complex_t | p | ||
| ) |
Extension of polar construction to complex.
| [in] | a | Magnitude |
| [in] | p | Angle |
Definition at line 566 of file complex.cpp.
| matvec qucs::pow | ( | matvec | , |
| vector | |||
| ) |
| nr_double_t qucs::pow | ( | const nr_double_t | a, |
| const nr_double_t | b | ||
| ) |
| nr_complex_t qucs::pow | ( | const nr_complex_t | z, |
| const nr_double_t | d | ||
| ) |
Compute power function with real exponent.
| [in] | z | complex mantisse |
| [in] | d | real exponent |
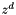 )
) Definition at line 238 of file complex.cpp.
| nr_complex_t qucs::pow | ( | const nr_double_t | d, |
| const nr_complex_t | z | ||
| ) |
Compute power function with complex exponent but real mantisse.
| [in] | d | real mantisse |
| [in] | z | complex exponent |
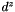 )
) Definition at line 248 of file complex.cpp.
| vector qucs::pow | ( | vector | , |
| const nr_complex_t | |||
| ) |
Definition at line 407 of file vector.cpp.
| vector qucs::pow | ( | vector | , |
| const nr_double_t | |||
| ) |
Definition at line 413 of file vector.cpp.
| vector qucs::pow | ( | const nr_complex_t | , |
| vector | |||
| ) |
Definition at line 419 of file vector.cpp.
| vector qucs::pow | ( | const nr_double_t | , |
| vector | |||
| ) |
Definition at line 425 of file vector.cpp.
| vector qucs::pow | ( | vector | , |
| vector | |||
| ) |
Definition at line 431 of file vector.cpp.
| nr_complex_t qucs::pow | ( | const nr_complex_t | z1, |
| const nr_complex_t | z2 | ||
| ) |
Compute complex power function.
| [in] | z1 | complex mantisse |
| [in] | z2 | complex exponent |
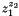 )
) Definition at line 258 of file complex.cpp.
| matvec qucs::pow | ( | matvec | a, |
| int | n | ||
| ) |
Definition at line 491 of file matvec.cpp.
| matvec qucs::pow | ( | matvec | a, |
| qucs::vector | v | ||
| ) |
Definition at line 498 of file matvec.cpp.
| matrix qucs::pow | ( | matrix | a, |
| int | n | ||
| ) |
Definition at line 632 of file matrix.cpp.
| nr_complex_t qucs::prod | ( | vector | ) |
Definition at line 257 of file vector.cpp.
| nr_double_t qucs::quadr | ( | const nr_double_t | r | ) |
| vector qucs::real | ( | vector | ) |
Definition at line 346 of file vector.cpp.
| nr_double_t qucs::real | ( | const nr_double_t | r | ) |
| matvec qucs::real | ( | matvec | a | ) |
Definition at line 535 of file matvec.cpp.
| matrix qucs::real | ( | matrix | a | ) |
Real part matrix.
| [in] | a | matrix |
add real in place
a is const
Definition at line 568 of file matrix.cpp.
| nr_double_t qucs::rollet | ( | matrix | ) |
| qucs::vector qucs::rollet | ( | matvec | m | ) |
Definition at line 668 of file matvec.cpp.
| vector qucs::round | ( | vector | ) |
Definition at line 1040 of file vector.cpp.
| nr_complex_t qucs::round | ( | const nr_complex_t | z | ) |
Complex round Round is the nearest integral value Apply round to real and imaginary part.
| [in] | z | complex number |
Definition at line 496 of file complex.cpp.
| vector qucs::rtoy | ( | vector | , |
| nr_complex_t | zref = 50.0 |
||
| ) |
Definition at line 584 of file vector.cpp.
| nr_complex_t qucs::rtoy | ( | const nr_complex_t | r, |
| nr_complex_t | zref | ||
| ) |
Converts reflexion coefficient to admittance.
| [in] | r | reflexion coefficient |
| [in] | zref | normalisation impedance |
Definition at line 608 of file complex.cpp.
| vector qucs::rtoz | ( | vector | , |
| nr_complex_t | zref = 50.0 |
||
| ) |
Definition at line 577 of file vector.cpp.
| nr_complex_t qucs::rtoz | ( | const nr_complex_t | r, |
| nr_complex_t | zref | ||
| ) |
Converts reflexion coefficient to impedance.
| [in] | r | reflexion coefficient |
| [in] | zref | normalisation impedance |
Definition at line 590 of file complex.cpp.
| qucs::vector qucs::runavg | ( | qucs::vector | , |
| const int | |||
| ) |
| qucs::vector qucs::runavg | ( | const nr_complex_t | , |
| const int | |||
| ) |
Definition at line 1222 of file vector.cpp.
| vector qucs::runavg | ( | vector | v, |
| const int | n | ||
| ) |
Definition at line 1228 of file vector.cpp.
| nr_type_t qucs::scalar | ( | tvector< nr_type_t > | a, |
| tvector< nr_type_t > | b | ||
| ) |
Definition at line 283 of file tvector.cpp.
| vector qucs::sech | ( | vector | ) |
Definition at line 514 of file vector.cpp.
| nr_complex_t qucs::sech | ( | const nr_complex_t | z | ) |
Compute complex hyperbolic secant.
| [in] | z | complex angle |
Definition at line 343 of file complex.cpp.
| vector qucs::sign | ( | vector | ) |
Definition at line 275 of file vector.cpp.
| nr_double_t qucs::sign | ( | const nr_double_t | d | ) |
| nr_complex_t qucs::sign | ( | const nr_complex_t | z | ) |
complex sign function
compute
![\[ \mathrm{sign}\;z= \mathrm{sign} (re^{i\theta}) = \begin{cases} 1 & \text{if } z=0 \\ e^{i\theta} & \text{else} \end{cases} \]](form_64.png)
| [in] | z | complex number |
Definition at line 435 of file complex.cpp.
| vector qucs::signum | ( | vector | ) |
Definition at line 269 of file vector.cpp.
| nr_double_t qucs::signum | ( | const nr_double_t | d | ) |
| nr_complex_t qucs::signum | ( | const nr_complex_t | z | ) |
complex signum function
compute
![\[ \mathrm{signum}\;z= \mathrm{signum} (re^{i\theta}) = \begin{cases} 0 & \text{if } z=0 \\ e^{i\theta} & \text{else} \end{cases} \]](form_63.png)
| [in] | z | complex number |
Definition at line 416 of file complex.cpp.
| nr_double_t qucs::sin | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::sin | ( | const nr_complex_t | z | ) |
Compute complex sine.
| [in] | z | complex angle |
Definition at line 66 of file complex.cpp.
| vector qucs::sin | ( | vector | ) |
Definition at line 448 of file vector.cpp.
| vector qucs::sinc | ( | vector | ) |
Definition at line 322 of file vector.cpp.
| nr_double_t qucs::sinc | ( | const nr_double_t | d | ) |
| nr_complex_t qucs::sinc | ( | const nr_complex_t | z | ) |
Cardinal sine.
Compute 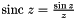
| [in] | z | complex number |
Definition at line 448 of file complex.cpp.
| nr_double_t qucs::sinh | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::sinh | ( | const nr_complex_t | z | ) |
Compute complex hyperbolic sine.
| [in] | z | complex arc |
Definition at line 144 of file complex.cpp.
| vector qucs::sinh | ( | vector | ) |
Definition at line 496 of file vector.cpp.
|
static |
Definition at line 334 of file nodelist.cpp.
| nr_double_t qucs::sqr | ( | const nr_double_t | r | ) |
| vector qucs::sqr | ( | vector | ) |
Definition at line 1046 of file vector.cpp.
| matvec qucs::sqr | ( | matvec | a | ) |
Definition at line 486 of file matvec.cpp.
| matrix qucs::sqr | ( | matrix | a | ) |
| nr_complex_t qucs::sqr | ( | const nr_complex_t | z | ) |
Square of complex number.
| [in] | z | complex number |
Definition at line 673 of file complex.cpp.
| nr_complex_t qucs::sqrt | ( | const nr_complex_t | z | ) |
Compute principal value of square root.
Compute the square root of a given complex number (except negative real), and with a branch cut along the negative real axis.
| [in] | z | complex number |
Definition at line 271 of file complex.cpp.
| vector qucs::sqrt | ( | vector | ) |
Definition at line 371 of file vector.cpp.
| vector qucs::step | ( | vector | ) |
Definition at line 1052 of file vector.cpp.
| nr_double_t qucs::step | ( | const nr_double_t | d | ) |
Heaviside step function.
The Heaviside step function, H, also called unit step function, is a discontinuous function whose value is zero for negative argument and one for positive argument. For zero by convention, H(0)=0.5
| [in] | d | Heaviside argument |
| nr_complex_t qucs::step | ( | const nr_complex_t | z | ) |
Heaviside step function for complex number.
Apply Heaviside to real and imaginary part
| [in] | z | Heaviside argument |
Create Heaviside alias
Why not using real heaviside
Definition at line 691 of file complex.cpp.
| matrix qucs::stoa | ( | matrix | s, |
| nr_complex_t | z1, | ||
| nr_complex_t | z2 | ||
| ) |
Converts chain matrix to scattering parameters.
Converts scattering parameters to chain matrix. Formulae are given by [5] tab 1. and are remembered here:
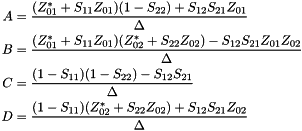
Where:
![\[ \Delta = 2 S_{21}\sqrt{\Re\text{e}\;Z_{01}\Re\text{e}\;Z_{02}} \]](form_97.png)
| [in] | s | Scattering matrix |
| [in] | z1 | impedance at input 1 |
| [in] | z2 | impedance at input 2 |
Definition at line 1181 of file matrix.cpp.
| matrix qucs::stog | ( | matrix | s, |
| nr_complex_t | z1, | ||
| nr_complex_t | z2 | ||
| ) |
Definition at line 1331 of file matrix.cpp.
| matrix qucs::stoh | ( | matrix | s, |
| nr_complex_t | z1, | ||
| nr_complex_t | z2 | ||
| ) |
Converts scattering parameters to hybrid matrix.
Converts chain matrix to scattering parameters Formulae are given by [5] and are remembered here:
Where  is:
is:
![\[ \Delta=(1-S_{11})(Z_{02}^*+S_{22}Z_{02})+S_{12}S_{21}Z_{02} \]](form_102.png)
| [in] | s | Scattering matrix |
| [in] | z1 | impedance at input 1 |
| [in] | z2 | impedance at input 2 |
Definition at line 1269 of file matrix.cpp.
| matvec qucs::stos | ( | matvec | , |
| vector | , | ||
| nr_complex_t | z0 = 50.0 |
||
| ) |
| matvec qucs::stos | ( | matvec | , |
| nr_complex_t | , | ||
| vector | |||
| ) |
| matvec qucs::stos | ( | matvec | , |
| vector | , | ||
| vector | |||
| ) |
| matrix qucs::stos | ( | matrix | , |
| vector | , | ||
| nr_complex_t | z0 = 50.0 |
||
| ) |
| matrix qucs::stos | ( | matrix | , |
| nr_complex_t | , | ||
| vector | |||
| ) |
| matrix qucs::stos | ( | matrix | , |
| vector | , | ||
| vector | |||
| ) |
| matvec qucs::stos | ( | matvec | s, |
| qucs::vector | zref, | ||
| qucs::vector | z0 | ||
| ) |
Definition at line 565 of file matvec.cpp.
| matvec qucs::stos | ( | matvec | s, |
| nr_complex_t | zref, | ||
| nr_complex_t | z0 | ||
| ) |
Definition at line 574 of file matvec.cpp.
| matvec qucs::stos | ( | matvec | s, |
| nr_double_t | zref, | ||
| nr_double_t | z0 | ||
| ) |
Definition at line 579 of file matvec.cpp.
| matvec qucs::stos | ( | matvec | s, |
| qucs::vector | zref, | ||
| nr_complex_t | z0 | ||
| ) |
Definition at line 583 of file matvec.cpp.
| matvec qucs::stos | ( | matvec | s, |
| nr_complex_t | zref, | ||
| qucs::vector | z0 | ||
| ) |
Definition at line 587 of file matvec.cpp.
| matrix qucs::stos | ( | matrix | s, |
| qucs::vector | zref, | ||
| qucs::vector | z0 | ||
| ) |
S params to S params.
Convert scattering parameters with the reference impedance 'zref' to scattering parameters with the reference impedance 'z0'.
Detail are given in [1], under equation (32)
New scatering matrix  is:
is:
![\[ S'=A^{-1}(S-\Gamma^+)(I-\Gamma S)^{-1}A^+ \]](form_72.png)
Where x^+ is the adjoint (or complex tranposate) of x, I the identity matrix and  is diagonal the matrix such as:
is diagonal the matrix such as:  and
and  the diagonal matrix such as:
the diagonal matrix such as:
![\[ A_i = \frac{(1-r_i^*)\sqrt{|1-r_ir_i^*|}}{|1-r_i|} \]](form_75.png)
Where  is the complex conjugate of
is the complex conjugate of 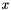 and
and 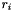 is wave reflexion coefficient of
is wave reflexion coefficient of 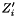 with respect to
with respect to 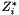 (where
(where 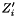 is the new impedance and
is the new impedance and 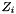 is the old impedance), ie:
is the old impedance), ie:
![\[ r_i = \frac{Z_i'-Z_i}{Z_i'-Z_i^*} \]](form_82.png)
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Correct documentation about standing waves [1-4]
Implement Speciale implementation [2-3] if applicable
s, zref and z0 const
Definition at line 890 of file matrix.cpp.
| matrix qucs::stos | ( | matrix | s, |
| nr_complex_t | zref, | ||
| nr_complex_t | z0 | ||
| ) |
S renormalization with all part identic.
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Definition at line 910 of file matrix.cpp.
| matrix qucs::stos | ( | matrix | s, |
| nr_double_t | zref, | ||
| nr_double_t | z0 | ||
| ) |
S renormalization with all part identic and real.
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Definition at line 923 of file matrix.cpp.
| matrix qucs::stos | ( | matrix | s, |
| qucs::vector | zref, | ||
| nr_complex_t | z0 | ||
| ) |
S renormalization (variation)
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Definition at line 935 of file matrix.cpp.
| matrix qucs::stos | ( | matrix | s, |
| nr_complex_t | zref, | ||
| qucs::vector | z0 | ||
| ) |
S renormalization (variation)
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Why not inline
s, zref and z0 const
Definition at line 947 of file matrix.cpp.
| matvec qucs::stoy | ( | matvec | , |
| vector | |||
| ) |
| matrix qucs::stoy | ( | matrix | , |
| vector | |||
| ) |
| matvec qucs::stoy | ( | matvec | s, |
| qucs::vector | z0 | ||
| ) |
Definition at line 592 of file matvec.cpp.
| matvec qucs::stoy | ( | matvec | s, |
| nr_complex_t | z0 | ||
| ) |
Definition at line 599 of file matvec.cpp.
| matrix qucs::stoy | ( | matrix | s, |
| qucs::vector | z0 | ||
| ) |
Scattering parameters to admittance matrix.
Convert scattering parameters to admittance matrix. According to [1] eq (19):
![\[ Z=F^{-1} (I- S)^{-1} (SG + G^+) F \]](form_83.png)
Where  is the scattering matrix,
is the scattering matrix,  is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
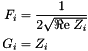
Using the well know formula 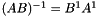 , we derivate:
, we derivate:
![\[ Y=F^{-1} (SG+G^+)^{-1} (I-S) F \]](form_93.png)
| [in] | s | Scattering matrix |
| [in] | z0 | Normalisation impedance |
 in
in  because we compute
because we compute 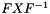 and therefore
and therefore  will simplify.
will simplify. Definition at line 1082 of file matrix.cpp.
| matrix qucs::stoy | ( | matrix | s, |
| nr_complex_t | z0 | ||
| ) |
Convert scattering pto adminttance parameters identic case.
| [in] | S | Scattering matrix |
| [in] | z0 | Normalisation impedance |
Why not inline
s and z0 const
Definition at line 1101 of file matrix.cpp.
| matvec qucs::stoz | ( | matvec | , |
| vector | |||
| ) |
| matrix qucs::stoz | ( | matrix | , |
| vector | |||
| ) |
| matvec qucs::stoz | ( | matvec | s, |
| qucs::vector | z0 | ||
| ) |
Definition at line 616 of file matvec.cpp.
| matvec qucs::stoz | ( | matvec | s, |
| nr_complex_t | z0 | ||
| ) |
Definition at line 623 of file matvec.cpp.
| matrix qucs::stoz | ( | matrix | s, |
| qucs::vector | z0 | ||
| ) |
Scattering parameters to impedance matrix.
Convert scattering parameters to impedance matrix. According to [1] eq (19):
![\[ Z=F^{-1} (I- S)^{-1} (SG + G^+) F \]](form_83.png)
Where  is the scattering matrix,
is the scattering matrix,  is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
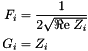
| [in] | s | Scattering matrix |
| [in] | z0 | Normalisation impedance |
 in
in  because we compute
because we compute  and therefore
and therefore 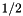 will simplify.
will simplify. Definition at line 973 of file matrix.cpp.
| matrix qucs::stoz | ( | matrix | s, |
| nr_complex_t | z0 | ||
| ) |
Scattering parameters to impedance matrix identic case.
| [in] | s | Scattering matrix |
| [in] | z0 | Normalisation impedance |
Why not inline?
s and z0 const?
Definition at line 992 of file matrix.cpp.
| nr_complex_t qucs::sum | ( | vector | ) |
Definition at line 251 of file vector.cpp.
| nr_type_t qucs::sum | ( | tvector< nr_type_t > | a | ) |
Definition at line 299 of file tvector.cpp.
| nr_double_t qucs::tan | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::tan | ( | const nr_complex_t | z | ) |
Compute complex tangent.
| [in] | z | complex angle |
Definition at line 75 of file complex.cpp.
| vector qucs::tan | ( | vector | ) |
Definition at line 472 of file vector.cpp.
| nr_double_t qucs::tanh | ( | const nr_double_t | arg | ) |
| nr_complex_t qucs::tanh | ( | const nr_complex_t | z | ) |
Compute complex hyperbolic tangent.
| [in] | z | complex arc |
Definition at line 153 of file complex.cpp.
| vector qucs::tanh | ( | vector | ) |
Definition at line 538 of file vector.cpp.
| tmatrix<nr_type_t> qucs::teye | ( | int | n | ) |
Definition at line 247 of file tmatrix.cpp.
| matrix qucs::transpose | ( | matrix | a | ) |
Matrix transposition.
| [in] | a | Matrix to transpose |
add transpose in place
a is const
Definition at line 492 of file matrix.cpp.
| matvec qucs::transpose | ( | matvec | a | ) |
Definition at line 557 of file matvec.cpp.
| nr_complex_t qucs::trunc | ( | const nr_complex_t | z | ) |
Complex trunc Apply round to integer, towards zero to real and imaginary part.
| [in] | z | complex number |
Definition at line 512 of file complex.cpp.
| matvec qucs::twoport | ( | matvec | m, |
| char | in, | ||
| char | out | ||
| ) |
Definition at line 658 of file matvec.cpp.
| matrix qucs::twoport | ( | matrix | m, |
| char | in, | ||
| char | out | ||
| ) |
Generic conversion matrix.
This function converts 2x2 matrices from any of the matrix forms Y, Z, H, G and A to any other. Also converts S<->(A, T, H, Y and Z) matrices. Convertion assumed:
Y->Y, Y->Z, Y->H, Y->G, Y->A, Y->S, Z->Y, Z->Z, Z->H, Z->G, Z->A, Z->S, H->Y, H->Z, H->H, H->G, H->A, H->S, G->Y, G->Z, G->H, G->G, G->A, G->S, A->Y, A->Z, A->H, A->G, A->A, A->S, S->Y, S->Z, S->H, S->G, S->A, S->S, S->T,T->T,T->S
| [in] | m | base matrix |
| [in] | in | matrix |
| [in] | out | matrix |
Definition at line 1594 of file matrix.cpp.
Definition at line 235 of file vector.cpp.
| vector qucs::w2dbm | ( | vector | ) |
Definition at line 1186 of file vector.cpp.
| nr_double_t qucs::xhypot | ( | const nr_double_t | a, |
| const nr_double_t | b | ||
| ) |
Euclidean distance function.
The xhypot() function returns 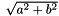 . This is the length of the hypotenuse of a right-angle triangle with sides of length a and b, or the distance of the point (a,b) from the origin.
. This is the length of the hypotenuse of a right-angle triangle with sides of length a and b, or the distance of the point (a,b) from the origin.
| [in] | a | first length |
| [in] | b | second length |
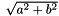
| vector qucs::xhypot | ( | vector | , |
| vector | |||
| ) |
Definition at line 305 of file vector.cpp.
| vector qucs::xhypot | ( | vector | , |
| const nr_complex_t | |||
| ) |
Definition at line 281 of file vector.cpp.
| vector qucs::xhypot | ( | vector | , |
| const nr_double_t | |||
| ) |
Definition at line 287 of file vector.cpp.
| vector qucs::xhypot | ( | const nr_complex_t | , |
| vector | |||
| ) |
Definition at line 293 of file vector.cpp.
| vector qucs::xhypot | ( | const nr_double_t | , |
| vector | |||
| ) |
Definition at line 299 of file vector.cpp.
| nr_double_t qucs::xhypot | ( | const nr_complex_t | a, |
| const nr_complex_t | b | ||
| ) |
Euclidean distance function for complex argument.
The xhypot() function returns 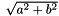 . This is the length of the hypotenuse of a right-angle triangle with sides of length a and b, or the distance of the point (a,b) from the origin.
. This is the length of the hypotenuse of a right-angle triangle with sides of length a and b, or the distance of the point (a,b) from the origin.
| [in] | a | first length |
| [in] | b | second length |
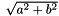
Definition at line 465 of file complex.cpp.
| nr_double_t qucs::xhypot | ( | nr_double_t | a, |
| nr_complex_t | b | ||
| ) |
Euclidean distance function for a double b complex.
Definition at line 478 of file complex.cpp.
| nr_double_t qucs::xhypot | ( | nr_complex_t | a, |
| nr_double_t | b | ||
| ) |
Euclidean distance function for b double a complex.
Definition at line 484 of file complex.cpp.
| vector qucs::yn | ( | const int | , |
| vector | |||
| ) |
Definition at line 1120 of file vector.cpp.
| nr_complex_t qucs::yn | ( | const int | n, |
| const nr_complex_t | z | ||
| ) |
Bessel function of second kind.
| [in] | n | order |
| [in] | z | argument |
Definition at line 742 of file complex.cpp.
| vector qucs::ytor | ( | vector | , |
| nr_complex_t | zref = 50.0 |
||
| ) |
Definition at line 570 of file vector.cpp.
| nr_complex_t qucs::ytor | ( | const nr_complex_t | y, |
| nr_complex_t | zref | ||
| ) |
Converts admittance to reflexion coefficient.
| [in] | y | admitance |
| [in] | zref | normalisation impedance |
Definition at line 599 of file complex.cpp.
| matvec qucs::ytos | ( | matvec | , |
| vector | |||
| ) |
| matrix qucs::ytos | ( | matrix | , |
| vector | |||
| ) |
| matvec qucs::ytos | ( | matvec | y, |
| qucs::vector | z0 | ||
| ) |
Definition at line 604 of file matvec.cpp.
| matvec qucs::ytos | ( | matvec | y, |
| nr_complex_t | z0 | ||
| ) |
Definition at line 611 of file matvec.cpp.
| matrix qucs::ytos | ( | matrix | y, |
| qucs::vector | z0 | ||
| ) |
Admittance matrix to scattering parameters.
Convert admittance matrix to scattering parameters. Using the same methodology as [1] eq (16-19), but writing (16) as 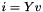 , ie
, ie
![\[ S=F(I-G^+Y)(I-GY)^{-1}F^{-1} \]](form_95.png)
Where  is the scattering matrix,
is the scattering matrix,  is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
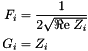
Using the well know formula 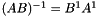 , we derivate:
, we derivate:
![\[ Y=F^{-1} (SG+G^+)^{-1} (I-S) F \]](form_93.png)
| [in] | y | admittance matrix |
| [in] | z0 | Normalisation impedance |
 in
in  because we compute
because we compute 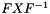 and therefore
and therefore  will simplify.
will simplify. Definition at line 1133 of file matrix.cpp.
| matrix qucs::ytos | ( | matrix | y, |
| nr_complex_t | z0 | ||
| ) |
Convert Admittance matrix to scattering parameters identic case.
| [in] | y | Admittance matrix |
| [in] | z0 | Normalisation impedance |
Why not inline
y and z0 const
Definition at line 1151 of file matrix.cpp.
| matvec qucs::ytoz | ( | matvec | y | ) |
Definition at line 648 of file matvec.cpp.
| matrix qucs::ytoz | ( | matrix | y | ) |
Convert admittance matrix to impedance matrix.
Convert  matrix to
matrix to  matrix using well known relation
matrix using well known relation 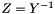
| [in] | y | admittance matrix |
Definition at line 1380 of file matrix.cpp.
| vector qucs::ztor | ( | vector | , |
| nr_complex_t | zref = 50.0 |
||
| ) |
Definition at line 563 of file vector.cpp.
| nr_complex_t qucs::ztor | ( | const nr_complex_t | z, |
| nr_complex_t | zref | ||
| ) |
Converts impedance to reflexion coefficient.
| [in] | z | impedance |
| [in] | zref | normalisation impedance |
Definition at line 581 of file complex.cpp.
| matvec qucs::ztos | ( | matvec | , |
| vector | |||
| ) |
| matrix qucs::ztos | ( | matrix | , |
| vector | |||
| ) |
| matvec qucs::ztos | ( | matvec | z, |
| qucs::vector | z0 | ||
| ) |
Definition at line 628 of file matvec.cpp.
| matvec qucs::ztos | ( | matvec | z, |
| nr_complex_t | z0 | ||
| ) |
Definition at line 635 of file matvec.cpp.
| matrix qucs::ztos | ( | matrix | z, |
| qucs::vector | z0 | ||
| ) |
Convert impedance matrix scattering parameters.
Convert scattering parameters to impedance matrix. According to [1] eq (18):
![\[ S=F(Z-G^+)(Z+G)^{-1} F^{-1} \]](form_89.png)
Where  is the scattering matrix,
is the scattering matrix,  is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
| [in] | Z | Impedance matrix |
| [in] | z0 | Normalisation impedance |
 in
in  because we compute
because we compute  and therefore
and therefore  will simplify.
will simplify. Definition at line 1018 of file matrix.cpp.
| matrix qucs::ztos | ( | matrix | z, |
| nr_complex_t | z0 | ||
| ) |
Convert impedance matrix to scattering parameters identic case.
| [in] | Z | Impedance matrix |
| [in] | z0 | Normalisation impedance |
Why not inline
z and z0 const
Definition at line 1037 of file matrix.cpp.
| matvec qucs::ztoy | ( | matvec | z | ) |
Definition at line 640 of file matvec.cpp.
| matrix qucs::ztoy | ( | matrix | z | ) |
impedance matrix to admittance matrix.
Convert impedance matrix to admittance matrix. By definition 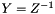
| [in] | z | impedance matrix |
Why not inline
z const
Definition at line 1050 of file matrix.cpp.
 1.8.6
1.8.6